Question

3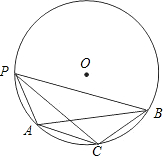．如图，点P为⊙O上一点，弦AB=$\sqrt{3}$cm，PC是∠APB的平分线，∠BAC=30°．
（Ⅰ）求⊙O的半径；
（Ⅱ）当∠PAC等于多少时，四边形PACB有最大面积？最大面积是多少？
（直接写出答案）

Answer 1

分析 （Ⅰ）连接OA，OC，根据圆周角定理得到∠AOC=60°，由角平分线的定义得到∠APC=∠BPC，求得$\widehat{AC}=\widehat{BC}$，得到AD=BD=$\frac{\sqrt{3}}{2}$，OC⊥AB，即可得到结论；
（Ⅱ）先求得AC=BC，再根据已知条件得S_{四边形PACB}=S_△ABC+S_△PABS_△ABC，当S_△PAB最大时，四边形PACB面积最大，求出PC=2，从而计算出最大面积．

解答 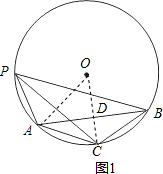解：（Ⅰ）如图1，连接OA，OC，
∵∠ABC=30°，
∴∠AOC=60°，
∵PC是∠APB的平分线，
∴∠APC=∠BPC，
∴$\widehat{AC}=\widehat{BC}$，
∴AD=BD=$\frac{\sqrt{3}}{2}$，OC⊥AB，
∴OA=1，
∴⊙O的半径为1；
（Ⅱ）如图2，∵PC平分∠APB，
∴∠APC=∠BPC，
∴AC=BC，
由AB=$\sqrt{3}$cm，求得AC=BC=1，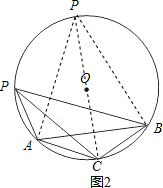
∵S_{四边形PACB}=S_△ABC+S_△PAB，
S_△ABC为定值，
当S_△PAB最大时，四边形PACB面积最大，
由图可知四边形PACB由△ABC和△PAB组成，
且△ABC面积不变，故要使四边形PACB面积最大，只需求出面积最大的△PAB即可，
在△PAB中，AB边不变，其最长的高为过圆心O与AB垂直（即AB的中垂线）与圆O交点P，此时四边形PACB面积最大．此时△PAB为等边三角形，此时PC应为圆的直径∠PAC=90°，
∵∠APC=∠BAC=30°，
∴PC=2AC=2，
∴四边形PACB的最大面积为$\frac{1}{2}$×$\sqrt{3}×2$=$\sqrt{3}$（cm²）．

点评 本题考查了垂径定理，圆周角定理，以及圆心角、弧、弦之间的关系，根据题意分类讨论是解题的关键．