题目内容
2．“校园手机”现象越来越受到社会的关注．“五一”期间，小记者刘铭随机调查了城区若干名学生和家长对中学生带手机现象的看法，统计整理并制作了如下的统计图：（1）求这次调查的家长人数，并补全图1；
（2）求图2中表示家长“赞成”的圆心角的度数；
（3）如果该市有8万名初中生，持“无所谓”态度的学生大约有多少人？
（4）从这次接受调查的家长与学生中随机抽查一个，恰好是“无所谓”态度的概率是多少？
分析 （1）利用条形图以及扇形统计图得出总人数即可；
（2）利用家长“赞成”所占比例进而得出其圆心角即可；
（3）利用持“无所谓”态度的学生所占比例，进而得出答案；
（4）利用“无所谓”态度的人数，进而求出其概率．
解答 解：（1）由题意可得出：80÷20%=400（人）；
家长反对人数：400-40-80=280（人）；
（2）家长“赞成”的圆心角的度数为：$\frac{40}{400}$×360°=36°；
（3）该市有8万名初中生，持“无所谓”态度的学生大约有：
80000×$\frac{30}{200}$=12000（人）；
（4）从这次接受调查的家长与学生中随机抽查一个，恰好是“无所谓”态度的概率是：$\frac{110}{400+200}$=$\frac{11}{60}$．
点评 此题主要考查了扇形统计图以及条形统计图的综合应用以及概率公式，利用条形图以及扇形图得出正确信息是解题关键．
练习册系列答案
天天向上一本好卷系列答案
相关题目
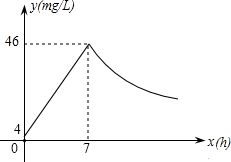近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO，在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4mg/L，此后浓度呈直线型增加，在第7小时达到最高值46mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降，如图所示，根据题中相关信息回答下列问题：
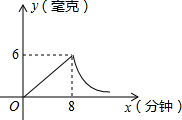为了预防流行性感冒，某学校对教室采用药熏消毒法进行消毒．已知药物燃烧时室内每立方米空气中的含药量y毫克）与时间x（分钟）成正比例；药物燃烧后，y与x成反比例（如图所示）．请根据图中提供的信息，解答下列问题：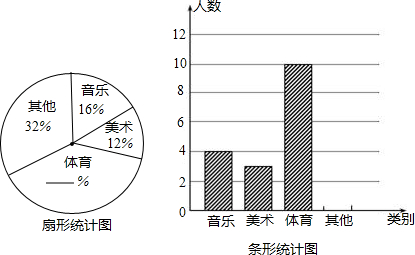
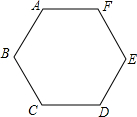17．
已知：如图在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y=$\frac{k}{x}$（x＞0）经过D点，交BC的延长线于E点，且OB•AC=160，则点E的坐标为（ ）
已知：如图在直角坐标系中，有菱形OABC，A点的坐标为（10，0），对角线OB、AC相交于D点，双曲线y=$\frac{k}{x}$（x＞0）经过D点，交BC的延长线于E点，且OB•AC=160，则点E的坐标为（ ）| A． | （5，8） | B． | （5，10） | C． | （4，8） | D． | （3，10） |
如图，已知点A、B、C、D、E、F是边长为1的正六边形的顶点，连接任意两点均可得到一条线段，在连接两点所得的所有线段中任取一条线段，取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$．
在平面直角坐标系中，已知点A（0，-3），点B（m，1），C（m+4，1）；