题目内容
11．
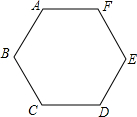如图，已知点A、B、C、D、E、F是边长为1的正六边形的顶点，连接任意两点均可得到一条线段，在连接两点所得的所有线段中任取一条线段，取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$．
分析 利用正六边形的性质以及勾股定理得出AE的长，进而利用概率公式求出即可．
解答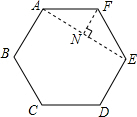 
解：连接AF，EF，AE，过点F作FN⊥AE于点N，
∵点A，B，C，D，E，F是边长为1的正六边形的顶点，
∴AF=EF=1，∠AFE=120°，
∴∠FAE=30°，
∴AN=$\frac{\sqrt{3}}{2}$，
∴AE=$\sqrt{3}$，同理可得：AC=$\sqrt{3}$，
故从任意一点，连接两点所得的所有线段一共有15种，任取一条线段，取到长度为$\sqrt{3}$的线段有6种情况，
则在连接两点所得的所有线段中任取一条线段，取到长度为$\sqrt{3}$的线段的概率为：$\frac{2}{5}$．
故答案为：$\frac{2}{5}$．
点评 此题主要考查了正多边形和圆以及几何概率，正确利用正六边形的性质得出AE的长是解题关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
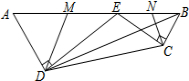如图，在四边形ABCD中，E为AB边上一点，ED⊥AD于D，EC⊥CB于C，且∠AED=∠BEC，AB=2$\sqrt{13}$，AD=3，BD=$\sqrt{37}$，M、N分别为AE、BE的中点，连接DM、CN，则△DEM与△CEN的周长之和为2$\sqrt{13}$+6．
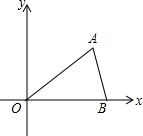如图，在平面直角坐标系中，点A（$\sqrt{3}$，1）、B（2，0）、O（0，0），反比例函数y=$\frac{k}{x}$图象过点A．
16．下列点中，位于函数y=$\frac{2}{x}$图象上的是（ ）
| A． | （1，2） | B． | （1，$\frac{1}{2}$） | C． | （1，1） | D． | （2，$\frac{1}{2}$） |
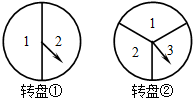某班举行联欢会，规定每个同学同时转动转盘①与转盘②（它们分别被二等分和三等分）．若两个转盘停止后，指针所指的数字之积为奇数，则这个同学要表演唱歌节目；若数字之积为偶数，则要表演其它节目．试求出转动转盘的同学表演唱歌节目的概率．（用树状图或列表方法求解）