题目内容
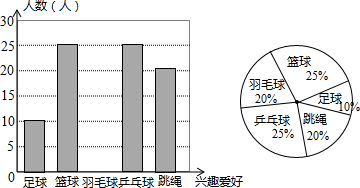
14.某校号召全校组件课外兴趣小组,学生会统计了某学期2-6月新注册的兴趣小组的数量,并将结果绘制成如下两种不完整的统计图:
(1)某学期2-6月新注册的兴趣小组一共有16个,请将折线图补充完整;
(2)4月新注册的小组中,有2个是绘画小组,现从4月新注册的小组中随机抽取2个小组了解其开展活动的情况,请你求出所抽取的2个小组恰好都是绘画的概率.
分析 (1)根据4月份有4个,占25%,可求出2-6月新注册的兴趣小组的总数,再求出2月份的数量,进而将折线统计图补充完整;
(2)设4月新注册的4小组为甲、乙、丙、丁,其中甲、乙为绘画小组,根据题意画出树状图,然后由树状图求得所有等可能的结果与甲、乙2个绘画小组恰好被抽到的情况,再利用概率公式求解即可求得答案.
解答 解:(1)根据统计图可知,4月份有4家,占25%,
所以某学期2-6月新注册的兴趣小组一共有:4÷25%=16(个),
2月份有:16-2-4-3-2=5(个),
补全折线统计图如下:
故答案为:16.
(2)设4月新注册的4小组为甲、乙、丙、丁,其中甲、乙为绘画小组.画树状图得:
∵共有12种等可能的结果,甲、乙2个小组恰好被抽到的有2种,
∴所抽取的2个小组恰好都是绘画的概率为:$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查了折线统计图、扇形统计图和列表法与树状图法,解决本题的关键是从两种统计图中整理出解题的有关信息,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
5.某城市自来水实行阶梯水价,收费标准如下表所示:
(1)若月用水量为xm3,水费为y元,求y与x的关系式;
(2)某用户4月份用水16m3,求所交水费;
(3)某用户5月份交水费45元,求所用水量.
| 月用水量 | 不超过12m3的部分 | 超过12m3的部分不超过18m3的部分 | 超过18m3的部分 |
| 收费标准(元/m3) | 2 | 2.5 | 3 |
(2)某用户4月份用水16m3,求所交水费;
(3)某用户5月份交水费45元,求所用水量.

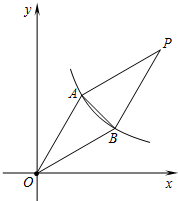 已知:如图,双曲线y=$\frac{k}{x}$在第一象限的分支经过A、B两点,点A的坐标为(2,2$\sqrt{3}$),点B的坐标为(m,2).
已知:如图,双曲线y=$\frac{k}{x}$在第一象限的分支经过A、B两点,点A的坐标为(2,2$\sqrt{3}$),点B的坐标为(m,2).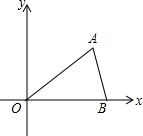 如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A.
如图,在平面直角坐标系中,点A($\sqrt{3}$,1)、B(2,0)、O(0,0),反比例函数y=$\frac{k}{x}$图象过点A.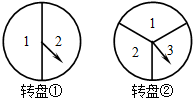 某班举行联欢会,规定每个同学同时转动转盘①与转盘②(它们分别被二等分和三等分).若两个转盘停止后,指针所指的数字之积为奇数,则这个同学要表演唱歌节目;若数字之积为偶数,则要表演其它节目.试求出转动转盘的同学表演唱歌节目的概率.(用树状图或列表方法求解)
某班举行联欢会,规定每个同学同时转动转盘①与转盘②(它们分别被二等分和三等分).若两个转盘停止后,指针所指的数字之积为奇数,则这个同学要表演唱歌节目;若数字之积为偶数,则要表演其它节目.试求出转动转盘的同学表演唱歌节目的概率.(用树状图或列表方法求解)