题目内容
17．设m、n是一元二次方程x2+2x-7=0的两个根，则m2+3m+n=5．分析 根据根与系数的关系可知m+n=-2，又知m是方程的根，所以可得m2+2m-7=0，最后可将m2+3m+n变成m2+2m+m+n，最终可得答案．
解答 解：∵设m、n是一元二次方程x2+2x-7=0的两个根，
∴m+n=-2，
∵m是原方程的根，
∴m2+2m-7=0，即m2+2m=7，
∴m2+3m+n=m2+2m+m+n=7-2=5，
故答案为：5．
点评 本题主要考查了根与系数的关系，解题的关键是把m2+3m+n转化为m2+2m+m+n的形式，结合根与系数的关系以及一元二次方程的解即可解答．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
5．
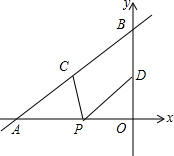如图，直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，当PC+PD最小时，点P的坐标为（ ）
如图，直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，当PC+PD最小时，点P的坐标为（ ）| A． | （-3，0） | B． | （-6，0） | C． | （-$\frac{3}{2}$，0） | D． | （-$\frac{5}{2}$，0） |
12．
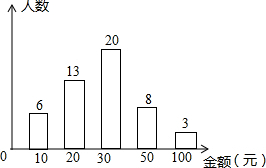随着智能手机的普及，抢微信红包成为了春节期间人们最喜欢的活动之一．某中学九年级五班班长对全班50名学生在春节期间所抢的红包金额进行统计，并绘制成了统计图．根据如图提供的信息，红包金额的众数和中位数分别是（ ）
随着智能手机的普及，抢微信红包成为了春节期间人们最喜欢的活动之一．某中学九年级五班班长对全班50名学生在春节期间所抢的红包金额进行统计，并绘制成了统计图．根据如图提供的信息，红包金额的众数和中位数分别是（ ）| A． | 20、20 | B． | 30、20 | C． | 30、30 | D． | 20、30 |
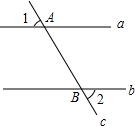如图，直线a∥b，直线c与直线a、b分别相交于A、B两点，若∠1=60°，则∠2=60°．
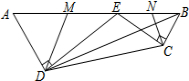如图，在四边形ABCD中，E为AB边上一点，ED⊥AD于D，EC⊥CB于C，且∠AED=∠BEC，AB=2$\sqrt{13}$，AD=3，BD=$\sqrt{37}$，M、N分别为AE、BE的中点，连接DM、CN，则△DEM与△CEN的周长之和为2$\sqrt{13}$+6．