题目内容
18.根据根与系数的关系,求下列方程的两根之和、两根之积:(1)x2+4x-5=0;
(2)2x2+4x=3.
分析 (1)直接根据x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$可得;
(2)整理成一般式后根据x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$可得.
解答 解:(1)∵a=1、b=4、c=-5,
∴x1+x2=-$\frac{b}{a}$=-4,x1x2=$\frac{c}{a}$=-5;
(2)整理,得:2x2+4x-3=0,
∵a=2,b=4,c=-3,
∴x1+x2=-$\frac{b}{a}$=-2,x1x2=$\frac{c}{a}$=-1.5.
点评 本题主要考查一元二次方程的根与系数的关系,熟练掌握x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$是解题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
8.一元二次方程2x2-2$\sqrt{6}$x+3=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
3.方程2x2-8=0的根是( )
| A. | x=2 | B. | x=-2 | C. | x1=2,x2=-2 | D. | x1=4,x2=-4 |
10.下列方程是一元二次方程的是 ( )
| A. | x-y2=1 | B. | $\frac{1}{{x}^{2}}$-1=0 | C. | 5(x-1)2=3(x+2)2+2x2 | D. | $\frac{{x}^{2}}{2}$-$\frac{x-1}{3}$=0 |
7.若关于x的一元二次方程kx2-10x+3=0有一个根为3,则k的值为( )
| A. | 11 | B. | -11 | C. | 3 | D. | -3 |
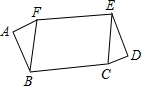 如图,已知BC=EF,BC∥EF,∠A=∠D,∠ABF=∠DEC,求证:AF=DC.
如图,已知BC=EF,BC∥EF,∠A=∠D,∠ABF=∠DEC,求证:AF=DC.