题目内容
4.用适当的方法解下列方程(1)x2-5x-6=0
(2)(x+2)2=3x+6
(3)x(x-3)=10
(4)2(x-2)2=x2-4
(5)(2x-1)(x+3)=4
(6)${x^2}-4\sqrt{2}x+8=0$.
分析 (1)把方程左边进行因式分解得到(x-6)(x+1)=0,然后解两个一元一次方程即可;
(2)把方程左边进行因式分解得到(x+2)(x+2-3)=0,然后解两个一元一次方程即可;
(3)把方程左边进行因式分解得到(x-5)(x+2)=0,然后解两个一元一次方程即可;
(4)把方程左边进行因式分解得到(x-2)(2x-4-x-2)=0,然后解两个一元一次方程即可;
(5)把方程左边进行因式分解得到(2x-7)(x+1)=0,然后解两个一元一次方程即可;
(6)把方程左边进行因式分解得到(x-2$\sqrt{2}$)2=0,然后解两个一元一次方程即可.
解答 解:(1)x2-5x-6=0
(x-6)(x+1)=0,
∴x-6=0,x+1=0,
∴x1=6,x2=-1;
(2)(x+2)2=3x+6
(x+2)2-3(x+2)=0
(x+2)(x+2-3)=0
∴x+2=0,x+2-3=0,
∴x1=-2,x2=1;
(3)x(x-3)=10
x2-3x-10=0,
(x-5)(x+2)=0,
∴x-5=0,x+2=0
∴x1=5,x2=-2;
(4)2(x-2)2=x2-4
2(x-2)2-(x+2)(x-2)=0
(x-2)(2x-4-x-2)=0,
∴x-2=0,x-6=0,
∴x1=2,x2=6;
(5)(2x-1)(x+3)=4
2x2+5x-7=0,
(2x-7)(x+1)=0,
∴2x-7=0,x+1=0,
∴x1=$\frac{7}{2}$,x2=-1;
(6)${x^2}-4\sqrt{2}x+8=0$
(x-2$\sqrt{2}$)2=0,
∴x1=x2=2$\sqrt{2}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

 阅读快车系列答案
阅读快车系列答案 如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,当AD=20m时,矩形场地的面积最大,最大值为800m2.
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,当AD=20m时,矩形场地的面积最大,最大值为800m2. 北京市在城市建设中,要折除旧烟囱AB,在烟囱正西方向的楼CD的顶端C,测得烟囱的顶端A的仰角为45°,底端B的俯角为30°,已量得DB=21m.拆除时若让烟囱向正东倒下,试问:距离烟囱东方35m远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
北京市在城市建设中,要折除旧烟囱AB,在烟囱正西方向的楼CD的顶端C,测得烟囱的顶端A的仰角为45°,底端B的俯角为30°,已量得DB=21m.拆除时若让烟囱向正东倒下,试问:距离烟囱东方35m远的一棵大树是否被歪倒的烟囱砸着?请说明理由. 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0),B(6,0),C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0),B(6,0),C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.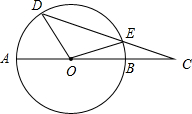 如图,已知AB是⊙O的直径,点D、E在⊙O上,且$\widehat{AD}$:$\widehat{DE}$=3:5,$\widehat{BE}$的度数为20°,连接DE并延长交AB的延长线于C,
如图,已知AB是⊙O的直径,点D、E在⊙O上,且$\widehat{AD}$:$\widehat{DE}$=3:5,$\widehat{BE}$的度数为20°,连接DE并延长交AB的延长线于C,