题目内容
13.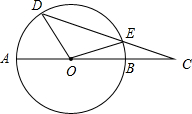 如图,已知AB是⊙O的直径,点D、E在⊙O上,且$\widehat{AD}$:$\widehat{DE}$=3:5,$\widehat{BE}$的度数为20°,连接DE并延长交AB的延长线于C,
如图,已知AB是⊙O的直径,点D、E在⊙O上,且$\widehat{AD}$:$\widehat{DE}$=3:5,$\widehat{BE}$的度数为20°,连接DE并延长交AB的延长线于C,(1)求∠AOD的度数;
(2)判断CE与AB有什么数量关系,并说明理由.
分析 (1)由AB是⊙O的直径,点D、E在⊙O上,且$\widehat{AD}$:$\widehat{DE}$=3:5,$\widehat{BE}$的度数为20°,可求得各弧的度数,继而求得其对的圆心角度数;
(2)由OD=OE,∠DOE=100°,可求得∠D的度数,然后由三角形外角的性质,求得∠C=∠EOC=20°,即可得CE=OE,继而求得答案.
解答 解:(1)∵$\widehat{AD}$:$\widehat{DE}$=3:5,$\widehat{BE}$的度数为20°,
∴$\widehat{AD}$的度数为60°,$\widehat{DE}$的度数为100°,
∴∠AOD=60°;
(2)CE=$\frac{1}{2}$AB.
理由:∵OD=OE,∠DOE=100°,
∴∠D=40°,
∴∠C=∠AOD-∠D=20°,
∴∠C=∠EOC=20°,
∴OE=CE,
∵OE=$\frac{1}{2}$AB,
∴CE=$\frac{1}{2}$AB.
点评 此题考查了圆心角与弧的关系、等腰三角形的判定与性质以及三角形外角的性质.注意求得各弧的度数是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列方程是一元二次方程的是( )
| A. | x+2y=1 | B. | x2+5=0 | C. | x2+$\frac{3}{x}$=8 | D. | 3x+8=6x+2 |
5.下列说法正确的是( )
| A. | -b是(-b)2的算术平方根 | B. | ±6是36的算术平方根 | ||
| C. | 5是25的算术平方根 | D. | -5是25的算术平方根 |
 已知:AE=DF,AE∥DF,CE=BF.求证:AB=CD.
已知:AE=DF,AE∥DF,CE=BF.求证:AB=CD.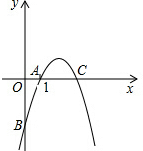 如图,抛物线y=-x2+5x+n经过点A(1,0),与x轴交于A、C两点,与y轴交于点B.
如图,抛物线y=-x2+5x+n经过点A(1,0),与x轴交于A、C两点,与y轴交于点B.