题目内容
 某公路有一个抛物线形状的隧道ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=-
某公路有一个抛物线形状的隧道ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=-| 1 |
| 10 |
(1)直接写出c=
(2)该隧道为双车道,现有一辆运货卡车高4米、宽3米,问这辆卡车能否顺利通过隧道?请说明理由;
(3)为了车辆安全快速通过隧道对该隧道加固维修,维修时需搭建的“脚手架”为矩形EFGH.使H、G点在抛物线上,E、F点在地面AB上.施工队最多需要筹备多少材料,(即求出“脚手架”三根木杆HE、HG、GF的长度之和的最大值)
考点:二次函数的应用
专题:
分析:(1)直接利用顶点C(0,5),进而求出c的值;
(2)利用x=3时,求出y的值,进而得出答案;
(3)利用HE=FG=-
x2+5,GH=EF=2x,即可得出HE+FG+GH与x的函数关系,进而求出最值即可.
(2)利用x=3时,求出y的值,进而得出答案;
(3)利用HE=FG=-
| 1 |
| 10 |
解答:解:(1)∵顶点C(0,5)
∴c=5,
故答案为:5.
(2)把x=3代入得y=-
x2+5=4.1>4,
故能安全通过;
(3)设F(x,0)则G(x,-
x2+5),
∴HE=FG=-
x2+5,GH=EF=2x,
∴HE+FG+GH=-
x2+2x+10
=-
(x-5)2+15(0<x<5
),
∴x=5时有最大值为15.
∴c=5,
故答案为:5.
(2)把x=3代入得y=-
| 1 |
| 10 |
故能安全通过;
(3)设F(x,0)则G(x,-
| 1 |
| 10 |
∴HE=FG=-
| 1 |
| 10 |
∴HE+FG+GH=-
| 1 |
| 5 |
=-
| 1 |
| 5 |
| 2 |
∴x=5时有最大值为15.
点评:此题主要考查了二次函数的应用,根据数形结合得出函数关系式是解题关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )
如图,AM、AN分别切⊙O于M、N两点,点B在⊙O上,且∠MBN=60°,则∠A的度数是( )| A、60° | B、70° |
| C、80° | D、140° |
 如图,在平面直角坐标系中,点O是坐标原点,四边形ABCD是菱形,点B、点C在x轴上,点A在y轴上,BD交y轴于点M,点A的坐标为(0,4),点B的坐标为(-3,0).
如图,在平面直角坐标系中,点O是坐标原点,四边形ABCD是菱形,点B、点C在x轴上,点A在y轴上,BD交y轴于点M,点A的坐标为(0,4),点B的坐标为(-3,0). 已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.
已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.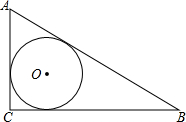 如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为c,a,b.求△ABC的内切圆半径r.
如图,Rt△ABC中,∠C=90°,AB,BC,CA的长分别为c,a,b.求△ABC的内切圆半径r.