题目内容
 已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.
已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接AC.(1)求证:AC平分∠EAD;
(2)猜想AB、AD、AF三条线段的数量关系,说明理由.
考点:切线的性质
专题:证明题
分析:(1)连接OC,如图1,根据切线的性质得OC⊥DE,而AD⊥EC,则OC∥AD,理由平行线的性质得∠OCA=∠DAC,加上∠OCA=∠OAC,所以∠OAC=∠DAC;
(2)连接CF、BC,BC的延长线交AD的延长线交于G,如图2,根据圆周角定理由AB为直径得∠ACB=90°,加上AC平分∠EAD,则可判断△ABG是等腰三角形,则AB=AG,CB=CG,利用∠BAC=∠FAC得到CB=CF,则CF=CG,而CD⊥FG,又可判断△FCG是等腰三角形,得到DF=DG,于是有AB+AF=AG+AF=AD+DG+AD-DF=2AD.
(2)连接CF、BC,BC的延长线交AD的延长线交于G,如图2,根据圆周角定理由AB为直径得∠ACB=90°,加上AC平分∠EAD,则可判断△ABG是等腰三角形,则AB=AG,CB=CG,利用∠BAC=∠FAC得到CB=CF,则CF=CG,而CD⊥FG,又可判断△FCG是等腰三角形,得到DF=DG,于是有AB+AF=AG+AF=AD+DG+AD-DF=2AD.
解答:(1)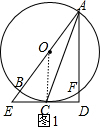 证明:连接OC,如图1,
证明:连接OC,如图1,
∵DE切⊙O于C,
∴OC⊥DE,
∵AD⊥EC,
∴OC∥AD,
∴∠OCA=∠DAC,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
∴AC平分∠EAD;
(2)解:AB+AF=2AD.理由如下:
连接CF、BC,BC的延长线交AD的延长线交于G,如图2,
∵AB为直径,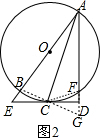
∴∠ACB=90°,
∴AC⊥BG,
∵AC平分∠EAD,
∴△ABG是等腰三角形,
∴AB=AG=AF+FG,CB=CG,
∵∠BAC=∠FAC,
∴CB=CF,
∴CF=CG,
而CD⊥FG,
∴△FCG是等腰三角形
∴DF=DG,
∴AB+AF=AG+AF=AD+DG+AD-DF=2AD.
 证明:连接OC,如图1,
证明:连接OC,如图1,∵DE切⊙O于C,
∴OC⊥DE,
∵AD⊥EC,
∴OC∥AD,
∴∠OCA=∠DAC,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
∴AC平分∠EAD;
(2)解:AB+AF=2AD.理由如下:
连接CF、BC,BC的延长线交AD的延长线交于G,如图2,
∵AB为直径,

∴∠ACB=90°,
∴AC⊥BG,
∵AC平分∠EAD,
∴△ABG是等腰三角形,
∴AB=AG=AF+FG,CB=CG,
∵∠BAC=∠FAC,
∴CB=CF,
∴CF=CG,
而CD⊥FG,
∴△FCG是等腰三角形
∴DF=DG,
∴AB+AF=AG+AF=AD+DG+AD-DF=2AD.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理、等腰三角形的判定与性质.

练习册系列答案
相关题目
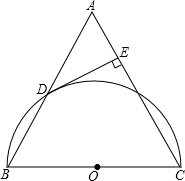 已知△ABC中,AB=AC,DE⊥AC于点E,DE与半⊙O相切于点D.
已知△ABC中,AB=AC,DE⊥AC于点E,DE与半⊙O相切于点D.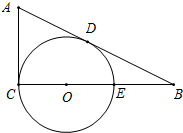 在△ABC中,∠ACB=90°,⊙O的圆心O在BC上,交BC于点C、E,且AB切⊙O于D,若OC:CB=1:3,AD=2,求BE.
在△ABC中,∠ACB=90°,⊙O的圆心O在BC上,交BC于点C、E,且AB切⊙O于D,若OC:CB=1:3,AD=2,求BE. 某公路有一个抛物线形状的隧道ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=-
某公路有一个抛物线形状的隧道ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=-