题目内容
6.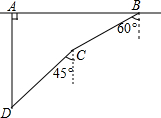 如图,一次军事演习中,蓝方在-条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截.红方行驶2000米到达C后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同距离,刚好在D处成功拦截蓝方.
如图,一次军事演习中,蓝方在-条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截.红方行驶2000米到达C后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同距离,刚好在D处成功拦截蓝方.(1)求点C到公路的距离;
(2)求红蓝双方最初的距离.(结果保留根号)
分析 过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°;
(1)点C到公路的距离就是BE的长,在Rt△BCE中,根据三角函数可求BE的长.
(2)红蓝双方相距AB=DF+CE.在Rt△BCE中,根据锐角三角函数的定义求出CE的长,同理,求出DF的长,进而可得出结论.
解答 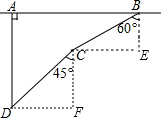 解:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,
解:过B作AB的垂线,过C作AB的平行线,两线交于点E;过C作AB的垂线,过D作AB的平行线,两线交于点F,则∠E=∠F=90°,
(1)点C到公路的距离就是BE的长,
在Rt△BCE中,∵BC=2000米,∠EBC=60°,
∴BE=BC•cos60°=2000×$\frac{1}{2}$=1000米.
答:点C到公路的距离就是BE的长是1000米.
(2)红蓝双方相距AB=DF+CE.
在Rt△BCE中,
∵BC=2000米,∠EBC=60°,
∴CE=BC•sin60°=2000×$\frac{\sqrt{3}}{2}$=1000$\sqrt{3}$米.
在Rt△CDF中,
∵∠F=90°,CD=2000米,∠DCF=45°,
∴DF=CD•sin45°=2000×$\frac{\sqrt{2}}{2}$=1000$\sqrt{2}$米,
∴AB=DF+CE=(1000$\sqrt{2}$+500$\sqrt{3}$)米.
答:红蓝双方最初相距(1000$\sqrt{2}$+1000$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,正确理解方向角的定义,进而作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
17.合肥市2017年中考的理化生实验操作考试已经顺利结束了,绝大部分同学都取得了满分成绩,某校对九年级20个班级的实验操作考试平均分x进行了分组统计,结果如下表所示:
(1)求a的值;
(2)若用扇形统计图来描述,求第三小组对应的扇形的圆心角度数;
(3)把在第二小组内的两个班分别记为:A1,A2,在第五小组内的三个班分别记为:B1,B2,B3,从第二小组和第五小组总共5个班级中随机抽取2个班级进行“你对中考实验操作考试的看法”的问卷调查,求第二小组至少有1个班级被选中的概率.
| 组号 | 分组 | 频数 |
| 一 | 9.6≤x<9.7 | 1 |
| 二 | 9.7≤x<9.8 | 2 |
| 三 | 9.8≤x<9.9 | a |
| 四 | 9.9≤x<10 | 8 |
| 五 | x=10 | 3 |
(2)若用扇形统计图来描述,求第三小组对应的扇形的圆心角度数;
(3)把在第二小组内的两个班分别记为:A1,A2,在第五小组内的三个班分别记为:B1,B2,B3,从第二小组和第五小组总共5个班级中随机抽取2个班级进行“你对中考实验操作考试的看法”的问卷调查,求第二小组至少有1个班级被选中的概率.
 如图,一次函数与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.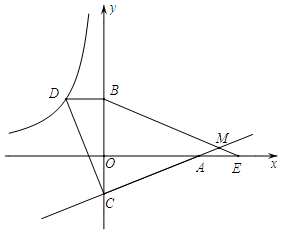 如图,已知点D在反比例函数y=$\frac{m}{x}$的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=$\frac{2}{5}$.
如图,已知点D在反比例函数y=$\frac{m}{x}$的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=$\frac{2}{5}$. 已知AB=AC,AD=AE,BA⊥AC,AD⊥AE,求证:BD=CE.
已知AB=AC,AD=AE,BA⊥AC,AD⊥AE,求证:BD=CE.