题目内容
6．下列说法中正确的是（ ）| A． | 两点之间的所有连线中，线段最短 | |
| B． | 射线比直线短 | |
| C． | 两条射线组成的图形叫角 | |
| D． | 小于平角的角可分为锐角和钝角两类 |
分析 根据线段、射线、角的概念及性质逐项分析即可．
解答 解：A．两点之间的所有连线中，线段最短，所以此选项正确；
B．射线和直线的长度均无法度量，所以无法比较长短，所以此选项错误；
C．有公共端点的两条射线组成的图形叫角，所以此选项错误；
D．小于平角的角可分为锐角和钝角两类，还应包括直角，所以次选项错误，
故选A．
点评 本题主要考查了线段、射线、角的概念及性质，理解概念是解答此题的关键．
练习册系列答案
相关题目
16．下列约分正确的是（ ）
| A． | $\frac{{a}^{6}}{{a}^{2}}$=a3 | B． | $\frac{a+x}{b+x}$=$\frac{a}{b}$ | C． | =a+b | D． | $\frac{-x-y}{x+y}$=-1 |
17．-2017的相反数是（ ）
| A． | -2017 | B． | -$\frac{1}{2017}$ | C． | $\frac{1}{2017}$ | D． | 2017 |
1．“养生薪春，中国艾都”，我县今年6月获得“中国艾都”称号，其中我县某公司生产的“时珍牌”艾条畅销国内外，该公司生产的艾条每盒成本为20元，其销售y（万盒）与销售价格x（元/盒）的变化如下表，销售过程中的其他开支（不含成本）总计40万元．
（1）观察并分析表格中y与x的对应关系，用学过的函数知识写出y与x的函数解析式；
（2）求出该公司生产，销售这种艾条的净利润z（万元）与销售价格x（元/盒）的函数关系式，并求出销售价格定位多少时净利润最大？最大值是多少？
（3）改公司要求净利润不低于40万元，请写出销售价格x（元/盒）的取值范围．
| 价格x（元/盒） | … | 30 | 40 | 50 | 60 | … |
| 销售量y（万盒） | … | 5 | 4 | 3 | 2 | … |
（2）求出该公司生产，销售这种艾条的净利润z（万元）与销售价格x（元/盒）的函数关系式，并求出销售价格定位多少时净利润最大？最大值是多少？
（3）改公司要求净利润不低于40万元，请写出销售价格x（元/盒）的取值范围．
11．
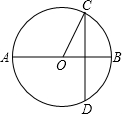如图，AB是⊙O的直径，弦CD⊥AB，∠OCD=30°，CD=2$\sqrt{3}$，则扇形BOC的面积为（ ）
如图，AB是⊙O的直径，弦CD⊥AB，∠OCD=30°，CD=2$\sqrt{3}$，则扇形BOC的面积为（ ）| A． | $\frac{2π}{3}$ | B． | $\frac{π}{3}$ | C． | π | D． | 2π |
18．
如图，梯形ABCD中，AD∥BC，DC⊥BC，将梯形沿对角线BD折叠，点A恰好落在DC边上的点A’处，若∠ABD=25°，则∠A′BC的度数为（ ）
如图，梯形ABCD中，AD∥BC，DC⊥BC，将梯形沿对角线BD折叠，点A恰好落在DC边上的点A’处，若∠ABD=25°，则∠A′BC的度数为（ ）| A． | 15° | B． | 20° | C． | 25° | D． | 30° |
15．
如图，在平面直角坐标系中，Rt△ABO中，∠ABO=90°，OB边在x轴上，将△ABO绕点B顺时针旋转60°得到△CBD．若点A的坐标为（-2，2$\sqrt{3}$），则点C的坐标为（ ）
如图，在平面直角坐标系中，Rt△ABO中，∠ABO=90°，OB边在x轴上，将△ABO绕点B顺时针旋转60°得到△CBD．若点A的坐标为（-2，2$\sqrt{3}$），则点C的坐标为（ ）| A． | （$\sqrt{3}$，1） | B． | （1，$\sqrt{3}$） | C． | （1，2） | D． | （2，1） |
16．下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上．相似的三角形是（ ）
| A． | ①和② | B． | ②和③ | C． | ①和③ | D． | ②和④ |