题目内容
18.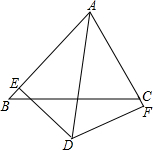 已知在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB于点E,DF⊥AC交AC的延长线于点F,求证:BE=CF.
已知在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB于点E,DF⊥AC交AC的延长线于点F,求证:BE=CF.
分析 连结BD,CD,由角平分线的性质和中垂线的性质就可以得出△BED≌△CFD,就可以得出结论.
解答 解:如图,连结BD,CD.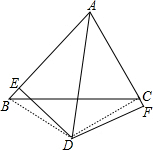
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠AED=∠BED=∠AFD=90°,DE=DF.
∵点D在BC的垂直平分线上,
∴DB=DC.
在Rt△DEB和Rt△DFC中,
$\left\{\begin{array}{l}{DB=DC}\\{DE=DF}\end{array}\right.$,
∴Rt△DEB≌Rt△DFC(HL),
∴BE=CF.
点评 本题考查了角平分线的性质的运用,垂直平分线的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
13.二元一次方程组$\left\{\begin{array}{l}{x+2y=1}\\{x-y=-2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ |
10.有A、B两个黑色袋子,A袋装有3个黑球、2个白球,B袋装有黑、白两个球,这些球除颜色外,其它一样.在随机抽球中,如果从A袋取一个球,再从B袋取一个球,那么得到两个都是黑球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{10}$ |
7.矩形的边长为10和15,其中一个内角平分线分长边为两部分,这两部分的长度分别为( )
| A. | 6和9 | B. | 5和10 | C. | 4和11 | D. | 7和8 |
 如图,正方形ABCD内有两点E、F满足AE=4,EF=FC=12,AE⊥EF,CF⊥EF,则正方形ABCD的边长为10$\sqrt{2}$.
如图,正方形ABCD内有两点E、F满足AE=4,EF=FC=12,AE⊥EF,CF⊥EF,则正方形ABCD的边长为10$\sqrt{2}$.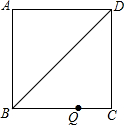 正方形ABCD的边长为6cm,点Q在边BC上,BQ=2QC.
正方形ABCD的边长为6cm,点Q在边BC上,BQ=2QC.