题目内容
13.阅读下列材料,解决后面两个问题:一个能被17整除的自然数我们称为“灵动数”.“灵动数”的特征是:若把一个整数的个位数字截去,再从余下的数中,减去个位数的5倍,如果差是17的整倍数(包括0),则原数能被17整除.如果差太大或心算不易看出是否是17的倍数,就继续上述的“截尾、倍大、相减、验差”的过程,直到能清楚判断为止.
例如:判断1675282能不能被17整除. 167528-2×5=167518,16751-8×5=16711,1671-1×5=1666,166-6×5=136,到这里如果你仍然观察不出来,就继续…6×5=30,现在个位×5=30>剩下的13,就用大数减去小数,30-13=17,17÷17=1;所以1675282能被17整除.
(1)请用上述方法判断7242和2098754 是否是“灵动数”,并说明理由;
(2)已知一个四位整数可表示为$\overline{27mn}$,其中个位上的数字为n,十位上的数字为m,0≤m≤9,0≤n≤9且m,n为整数.若这个数能被51整除,请求出这个数.
分析 (1)根据“灵动数”的特征,列出算式求解即可;
(2)先求出51×52<2700,51×55>2800,根据整数的定义求出51×53,51×54的积,从而求解.
解答 解:(1)724-2×5=714,71-4×5=51,51÷17=3,
所以7242能被17整除,是“灵动数”;
209875-4×5=209855,20985-5×5=20960,2096-0×5=2096,209-6×5=179,179÷17=10…9,
所以209875不能被17整除,不是“灵动数”;
(2)∵51×52<2700,51×55>2800,
51×53=2703,51×54=2754,
∴这个数是2703或2754.
点评 此题主要考查了新定义,数的整除,解本题的关键是理解新定义,掌握数的整除是解本题的难点.

练习册系列答案
相关题目
1.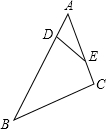 如图,在△ABC中,点D、E分别在AB、AC边上,且AD=2,AE=4,BD=10,CE=2,则DE:BC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,且AD=2,AE=4,BD=10,CE=2,则DE:BC等于( )
 如图,在△ABC中,点D、E分别在AB、AC边上,且AD=2,AE=4,BD=10,CE=2,则DE:BC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,且AD=2,AE=4,BD=10,CE=2,则DE:BC等于( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 1:5 |
8.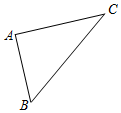 如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )
如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )
 如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )
如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
18.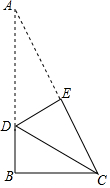 如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )
如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )
 如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )
如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )| A. | $\frac{7}{8}$ | B. | 1 | C. | $\frac{9}{8}$ | D. | $\frac{2}{3}$ |
5.点M(-4,-1)关于y轴对称的点的坐标为( )
| A. | (-4,1) | B. | (4,1) | C. | (4,-1) | D. | (-4,-1) |
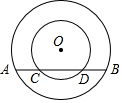 如图,两个同心圆,大圆半径为10cm,小圆的半径为6cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是16<AB≤20.
如图,两个同心圆,大圆半径为10cm,小圆的半径为6cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是16<AB≤20. 如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C,D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF的值为( )
如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C,D,E,F,$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF的值为( )