题目内容
8. 如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )
如图,在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,则cosB等于( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
分析 根据sinB的值结合sin2B+cos2B=1即可得出cosB的值,此题得解.
解答 解:∵在△ABC中,∠A=90°,sinB=$\frac{4}{5}$,
∴cosB=$\sqrt{1-si{n}^{2}B}$=$\sqrt{1-(\frac{4}{5})^{2}}$=$\frac{3}{5}$.
故选D.
点评 本题考查了同角三角函数的关系,熟练掌握同角的正、余弦值的平方和为1是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
17.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓线DFE所在抛物线的函数解析式为( )
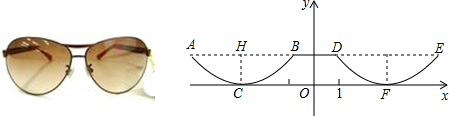

| A. | $y=\frac{1}{4}{(x+3)^2}$ | B. | $y=-\frac{1}{4}{(x+3)^2}$ | C. | $y=-\frac{1}{4}{(x-3)^2}$ | D. | $y=\frac{1}{4}{(x-3)^2}$ |
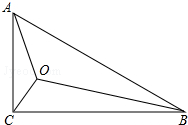 在Rt△ABC中,∠ACB=90°,AC=1,BC=$\sqrt{3}$,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=$\sqrt{7}$.
在Rt△ABC中,∠ACB=90°,AC=1,BC=$\sqrt{3}$,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=$\sqrt{7}$.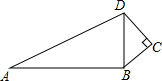 如图,已知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=13.
如图,已知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=13.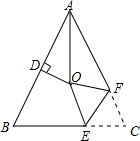 如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为( )
如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为( )