题目内容
17.如图①,直线y=-$\frac{1}{2}$x+1分别与坐标轴交于A,B两点,在y轴的负半轴上截取OC=OB(1)求直线AC的解析式;
(2)如图②,在x轴上取一点D(1,0),过D作DE⊥AB交y轴于E,求E点坐标.
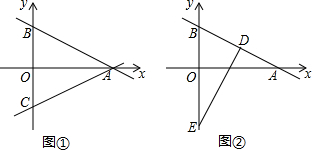
分析 (1)先求点A、B的坐标,根据在y轴的负半轴上截取OC=OB,得到点C的坐标为(0,-1),利用待定系数法求直线AC的解析式,即可解答;
(2)由直线AB的解析式为y=-$\frac{1}{2}$x+1,DE⊥AB,设直线DE的解析式为y=$\frac{1}{2}$x+b,把D(1,0)代入得:$\frac{1}{2}+$b=0,解得:b=-$\frac{1}{2}$,从而得到直线DE的解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,当x=0时,y=-$\frac{1}{2}$,即可确定点E的坐标为(0,-$\frac{1}{2}$).
解答 解:(1)y=-$\frac{1}{2}$x+1,
当x=0时,y=1,
当y=0时,x=2,
则点A的坐标为(2,0),点B的坐标为(0,1),
∵在y轴的负半轴上截取OC=OB,
∴点C的坐标为(0,-1),
设直线AC的解析式为y=kx+b,
把点A(2,0),C(0,-1)代入得:$\left\{\begin{array}{l}{2k+b=0}\\{b=-1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-1}\end{array}\right.$
∴y=$\frac{1}{2}$x-1.
(2)由直线AB的解析式为y=-$\frac{1}{2}$x+1,DE⊥AB,
设直线DE的解析式为y=$\frac{1}{2}$x+b,
把D(1,0)代入得:$\frac{1}{2}+$b=0,
解得:b=-$\frac{1}{2}$,
∴直线DE的解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,
当x=0时,y=-$\frac{1}{2}$,
∴点E的坐标为(0,-$\frac{1}{2}$).
点评 本题考查了一次函数的应用,解决本题的关键是利用待定系数法求函数的解析式.

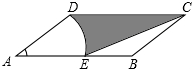 如图,在?ABCD中,BC=10,DC=12,∠B=150°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是55-$\frac{25}{3}$π(结果不取近似值)
如图,在?ABCD中,BC=10,DC=12,∠B=150°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是55-$\frac{25}{3}$π(结果不取近似值)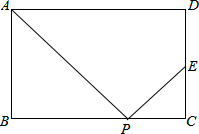 在矩形ABCD中,AB=4,AD=5,P是BC上的一点,E为CD上一点,且∠BAP=∠EPC,PE=DE.
在矩形ABCD中,AB=4,AD=5,P是BC上的一点,E为CD上一点,且∠BAP=∠EPC,PE=DE.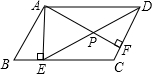 如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=3,CF=1.5,求AB,AF,DE的长.
如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=3,CF=1.5,求AB,AF,DE的长.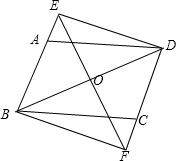 如图,点O为平行四边形ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E、F,求证:四边形BFDE是平行四边形.
如图,点O为平行四边形ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E、F,求证:四边形BFDE是平行四边形.