题目内容
6.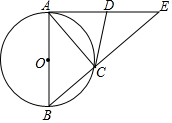 已知△ABE中,∠BAE=90°,以AB为直径作⊙O,与BE边相交于点C,过点C作⊙O的切线CD,交AE于点D.
已知△ABE中,∠BAE=90°,以AB为直径作⊙O,与BE边相交于点C,过点C作⊙O的切线CD,交AE于点D.(1)求证:D是AE的中点;
(2)求证:AE2=EC•EB.
分析 (1)根据已知条件得到AE为⊙O的切线,根据切线的性质得到AD=CD,由等腰三角形的性质得到∠DAC=∠DCA,由圆周角定理得到∠ACB=90°,根据余角的性质得到∠DCE=∠DEC,即可得到结论;
(2)根据圆周角定理得到∠ACB=90°,根据相似三角形的判定和性质即可得到结论.
解答 (1)证明:∵∠BAE=90°,AB为直径,
∴AE为⊙O的切线,
又CD为⊙O的切线,
∴AD=CD,
∴∠DAC=∠DCA,
又AB直径,
∴∠ACB=90°,
∴∠ACD+∠DCE=90°,∠DAC+∠DEC=90°,
∴∠DCE=∠DEC,
∴DC=DE,
∴AD=DE,
即D是AE的中点;
(2)解:∵∠BAE=90°,
∴∠BAC+∠CAE=90°,
又AB直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°,
∴∠CAE=∠ABC,
又∠E=∠E,
∴△ACE∽△BAE,
∴$\frac{AE}{BE}$=$\frac{CE}{AE}$,
∴AE2=EC•EB.
点评 本题考查了相似三角形的判定和性质,切线的判定和性质,余角的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
14.2016年我国新能源汽车产量达51.7万辆,居世界第一,将51.7万用科学记数法表示为( )
| A. | 5.17×103 | B. | 51.7×104 | C. | 5.17×105 | D. | 5.17×106 |
11.节约是一种美德,节约是一种智慧,据不完全统计,全国每年浪费的食物若折合成粮食可养活约360000000人,把350000000用科学记数法可以表示为( )
| A. | 3.5×1010 | B. | 3.5×109 | C. | 3.5×108 | D. | 3.5×107 |
15.若一个正比例函数的图象经过点(-2,1),则这个图象也一定经过点( )
| A. | (-$\frac{1}{2}$,1) | B. | (2,-1) | C. | (-1,2) | D. | (1,$\frac{1}{2}$) |
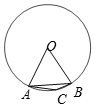 如图,在⊙O中,圆周角∠ACB=150°,弦AB=4,则扇形OAB的面积是$\frac{8}{3}$π.
如图,在⊙O中,圆周角∠ACB=150°,弦AB=4,则扇形OAB的面积是$\frac{8}{3}$π.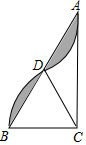 如图,在Rt△ABC中,∠ACB=90°,AC=4$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为$\frac{16}{3}$π-8$\sqrt{3}$.
如图,在Rt△ABC中,∠ACB=90°,AC=4$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为$\frac{16}{3}$π-8$\sqrt{3}$.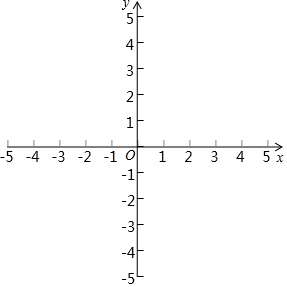 在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆”
在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆” 如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P90的坐标是(30,0).
如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P90的坐标是(30,0).