题目内容
1. 在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆”
在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆”(1)已知点P的坐标为(2,0)
①若点Q的坐标为(0,1),求点P、Q的“相关圆”的面积;
②若点Q的坐标为(3,n),且点P、Q的“相关圆”的半径为$\sqrt{5}$,求n的值;
(2)已知△ABC为等边三角形,点A和点B的坐标分别为(-$\sqrt{3}$,0)、($\sqrt{3}$,0),点C在y轴正半轴上,若点P、Q的“相关圆”恰好是△ABC的内切圆且点Q在直线y=2x上,求点Q的坐标.
(3)已知△ABC三个顶点的坐标为:A(-3,0)、B($\frac{9}{2}$,0),C(0,4),点P的坐标为(0,$\frac{3}{2}$),点Q的坐标为(m,$\frac{3}{2}$),若点P、Q的“相关圆”与△ABC的三边中至少一边存在公共点,直接写出m的取值范围.
分析 (1)①根据PQ=$\sqrt{O{P}^{2}+O{Q}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,求出⊙P的半径即可解决问题;
②过点Q作QH⊥x轴于H.利用勾股定理求出QH的值,即可解决问题;
(2)在Rt△OAC中,∠ACO=30°,可得OC=$\sqrt{3}$OA=3,推出C点坐标为(0,3),推出△ABC的内切圆的圆心的坐标为(0,1),半径为1,推出P(0,1),设Q(x,2x),则有x2+(2x-1)2=1,求出x即可;
(3)①当相关圆与AC、AB相切时,可得半径有最小值$\frac{3}{2}$.
②当相关圆经过点B时,可得半径最大值$\frac{3}{2}$$\sqrt{10}$,由此即可解决问题;
解答 解:(1)①∵PQ=$\sqrt{O{P}^{2}+O{Q}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴S=π•r2=5π.
②过点Q作QH⊥x轴于H.
∵HQ=$\sqrt{P{Q}^{2}-P{H}^{2}}$=2,
∴Q点坐标为(3,2)或(3,-2).
∴n=2或-2.
(2)如图,
在Rt△OAC中,∠ACO=30°,
∴OC=$\sqrt{3}$OA=3,
∴C点坐标为(0,3),
∴△ABC的内切圆的圆心的坐标为(0,1),半径为1,
∴P(0,1),
设Q(x,2x),则有x2+(2x-1)2=1,
解得x=$\frac{4}{5}$,
∴Q($\frac{4}{5}$,$\frac{8}{5}$).
(3)如图3中,
①当相关圆与AC、AB相切时半径有最小值$\frac{3}{2}$.
②当相关圆经过点B时,半径有最大值$\frac{3}{2}$$\sqrt{10}$,
∴-$\frac{3\sqrt{10}}{2}$≤m≤-$\frac{3}{2}$,$\frac{3}{2}$≤m≤$\frac{3\sqrt{10}}{2}$.
点评 本题考查圆综合题、切线的性质、勾股定理、点P、Q的“相关圆”的定义等知识,解题的关键是理解题意,灵活应用所学知识解决问题,属于中考压轴题.

| A. | 4(x4-16) | B. | (2x2+8)(2x2-8) | C. | 4(x2+4)(x2-4) | D. | 4(x2+4)(x+2)(x-2) |
| A. | $\frac{2}{x+1}$ | B. | $\frac{2}{x-1}$ | C. | -$\frac{2}{x+1}$ | D. | -$\frac{2}{x-1}$ |
| A. | k>0 | B. | k<0 | C. | k>1 | D. | k<1 |
| A. | 相反数 | B. | 绝对值 | C. | 平方数 | D. | 倒数 |
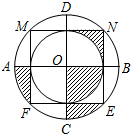 如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.
如图,边长为2的正方形MNEF的四个顶点分在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,小明随意向水平放置的该圆形区域内抛一个小球,则小球停在该图中阴影部分区域的概率为$\frac{1}{4}$.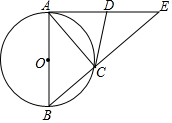 已知△ABE中,∠BAE=90°,以AB为直径作⊙O,与BE边相交于点C,过点C作⊙O的切线CD,交AE于点D.
已知△ABE中,∠BAE=90°,以AB为直径作⊙O,与BE边相交于点C,过点C作⊙O的切线CD,交AE于点D.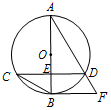 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AF=5,cos∠BCD=$\frac{3}{4}$.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AF=5,cos∠BCD=$\frac{3}{4}$.