题目内容
已知抛物线y=-2x2+8x-9的顶点为A,若二次函数y=ax2+bx+c的图象经过A点,且与x轴交于B(0,0)、C(3,0)两点,试求这个二次函数的解析式.
考点:待定系数法求二次函数解析式
专题:计算题
分析:先把y=-2x2+8x-9配成顶点式得到A点坐标为(2,-1),由于已知二次函数y=ax2+bx+c的图象与x轴的两交点坐标,则可设交点式y=ax(x-3),然后把A点坐标代入求出a的值即可.
解答:解:∵y=-2x2+8x-9=-2(x-2)2-1,
∴A点坐标为(2,-1),
设所求二次函数解析式为y=ax(x-3),
把A(2,-1)代入得a•2•(2-3)=-1,解得a=
,
∴所求二次函数解析式为y=
x(x-3)=
x2-
x.
∴A点坐标为(2,-1),
设所求二次函数解析式为y=ax(x-3),
把A(2,-1)代入得a•2•(2-3)=-1,解得a=
| 1 |
| 2 |
∴所求二次函数解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了轴对称-最短路线问题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
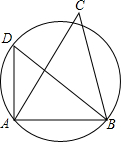 已知在相对灯塔A、B的张角为56°的弓形海域内有一暗礁群,如图,某海监执法大队正在对灯塔A,B的张角为55°的C处巡航维权,试问是否会有触礁的危险.
已知在相对灯塔A、B的张角为56°的弓形海域内有一暗礁群,如图,某海监执法大队正在对灯塔A,B的张角为55°的C处巡航维权,试问是否会有触礁的危险.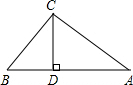 如图,在Rt△ABC中,∠BCA=90°,CD⊥AB,AD=2,CD=2
如图,在Rt△ABC中,∠BCA=90°,CD⊥AB,AD=2,CD=2 同学们都知道五月的第二个星期天是“母亲节”,小聪和妈妈一起去商场购物,他们发现商场现在举行促销打折活动(信息如图所示),小聪和妈妈给奶奶买了300元的营养品,让小聪结账.小聪在收银台旁发现有妈妈最喜欢的百合花,价格是2.5元钱一枝,他最多能买几枝又不需要多花钱呢?
同学们都知道五月的第二个星期天是“母亲节”,小聪和妈妈一起去商场购物,他们发现商场现在举行促销打折活动(信息如图所示),小聪和妈妈给奶奶买了300元的营养品,让小聪结账.小聪在收银台旁发现有妈妈最喜欢的百合花,价格是2.5元钱一枝,他最多能买几枝又不需要多花钱呢? 根据主视图和俯视图画出左视图.
根据主视图和俯视图画出左视图. 如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则cos∠CPB的值是
如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则cos∠CPB的值是