题目内容
3. 如图,点O为平面直角坐标系的原点,点A的坐标为(6,8),点B的坐标为(12,0).
如图,点O为平面直角坐标系的原点,点A的坐标为(6,8),点B的坐标为(12,0).(1)求证:AO=AB;
(2)用直尺和圆规作出△AOB的外心P;
(3)求点P的坐标.
分析 (1)利用;两点间的距离公式求出OA和AB,即可得出结论;
(2)由于点P是△AOB的外心,即:点P是△AOB的三边的垂直平分线的交点,进而用作垂直平分线的方法作出OB,OA的垂直平分线,交点即为点P;
(3)由OA=AB得出点P的横坐标和点A的横坐标相同,进而设出点P的坐标,再利用点P到点O和点A的距离线段建立方程求解即可.
解答 解:(1)∵点A的坐标为(6,8),
∴OA=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵点A的坐标为(6,8),点B的坐标为(12,0),
∴AB=$\sqrt{(12-6)^{2}+(-8)^{2}}$=10,
∴AO=AB;
(2)如图1,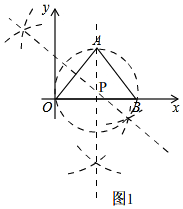
∴点P是所求作的△AOB的外心;
(3)如图2,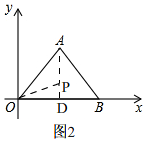
过点A作AD⊥OB于D,
连接OP,
∵点P是△AOB的外心,
∴PA=PO,
由(1)知,OA=AB,
∵A(6,8),
∴设P(6,m),
∴PA=8-m,PO=$\sqrt{{6}^{2}+{m}^{2}}$,
∴8-m=$\sqrt{{6}^{2}+{m}^{2}}$,
∴m=$\frac{7}{4}$,
∴P(6,$\frac{7}{4}$).
点评 此题主要考查了平面坐标系中,两点间的距离公式,三角形的外心的性质,基本作图;解本题的关键是作出点P,也是解本题的难点.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
13.把方程x2-6x+4=0的左边配成完全平方,正确的变形是( )
| A. | (x-3)2=9 | B. | (x-3)2=13 | C. | (x+3)2=5 | D. | (x-3)2=5 |
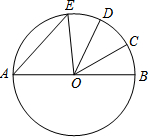 如图,AB是⊙O的直径,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=34°,则∠AEO的度数是51°.
如图,AB是⊙O的直径,$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$,∠COD=34°,则∠AEO的度数是51°. 如图,抛物线顶点坐标为点C(2,8),交x轴于点A(6,0),交y轴于点B.
如图,抛物线顶点坐标为点C(2,8),交x轴于点A(6,0),交y轴于点B. 如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE的度数为90°.
如图,已知AB⊥BD,ED⊥BD,AB=CD,AC=CE,则∠ACE的度数为90°. 如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF. 如图,点C在线段AB上,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,点M、N分别是AC、BC的中点. 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-5,0),对称轴为直线x=-2,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-5,0),对称轴为直线x=-2,给出四个结论: