题目内容
15. 如图,点C在线段AB上,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,点M、N分别是AC、BC的中点.(1)若AC=9cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?请直接写出你的答案.
(3)若C在线段AB的延长线上,且满足AC-BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
分析 (1)由中点的性质得MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,根据MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)可得答案;
(2)与(1)同理;
(3)根据中点的性质得MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,结合图形依据MN=MC-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)可得答案.
解答 解:(1)∵M、N分别是AC、BC的中点,
∴MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,
∵AC=9cm,CB=6cm,
∴MN=MC+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$(9+6)=7.5cm;
(2)∵M、N分别是AC、BC的中点,
∴MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,
∵AC+CB=acm,
∴MN=MC+CN=AC+CB=acm)=$\frac{1}{2}$a(cm);
(3)MN=$\frac{1}{2}$b,
如图,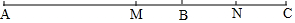
∵M、N分别是AC、BC的中点,
∴MC=$\frac{1}{2}$AC、CN=$\frac{1}{2}$BC,
∵AC-BC=b cm,
∴MN=MC-CN=$\frac{1}{2}$AC-$\frac{1}{2}$BC=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$b.
点评 本题主要考查两点间的距离,掌握线段的中点的性质、线段的和差运算是解题的关键.

练习册系列答案
相关题目
10.如果代数式$\frac{x-1}{\sqrt{x+2}}$有意义,则x的取值范围是( )
| A. | x≥-2 | B. | x>-2 | C. | x<-2 | D. | x≤-2 |
7.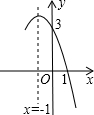 抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )
 抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )
抛物线y=-x2+bx+c的部分图象如图所示,对称轴为x=-1,若y>0,则x的取值范围是( )| A. | -3<x<1 | B. | x<-3或x>1 | C. | -4<x<l | D. | x<-4或x>1 |
5. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )| A. | $\sqrt{6}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
 如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BFA=34°,则∠DAE=17度.
如图,将长方形ABCD沿AE折叠,使点D落在BC边上的点F,若∠BFA=34°,则∠DAE=17度. 如图,点O为平面直角坐标系的原点,点A的坐标为(6,8),点B的坐标为(12,0).
如图,点O为平面直角坐标系的原点,点A的坐标为(6,8),点B的坐标为(12,0).