题目内容
11.(1)化简$\frac{{a}^{2}}{a-1}$+$\frac{1}{1-a}$(2)解方程(x+1)(x+3)=8.
分析 (1)先进行同分母的减法运算,然后把分子因式分解后约分即可;
(2)先把方程化为一般式,然后利用因式分解法解方程.
解答 解:(1)原式=$\frac{{a}^{2}}{a-1}$-$\frac{1}{a-1•}$
=$\frac{{a}^{2}-1}{a-1}$
=$\frac{(a+1)(a-1)}{a-1}$
=a+1;
(2)x2+4x-5=0,
(x+5)(x-1)=0,
x+5=0或x-1=0,
所以x1=-5,x2=1
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了分式的加减运算.

练习册系列答案
相关题目
16. 某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
(1)在频数分布表中,a=60,b=0.05;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
 某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
3.若$\sqrt{a+b+5}$与|2a-b+1|互为相反数,则(b-a)2017的值为( )
| A. | -1 | B. | 1 | C. | 52015 | D. | -52015 |
20.不等式组$\left\{\begin{array}{l}{2x+3<1}\\{2(x-2)>3x}\end{array}\right.$的解集是( )
| A. | x<-2 | B. | x<-4 | C. | -4<x<-2 | D. | 无解 |
1.在函数y=$\frac{2}{\sqrt{x-5}}$中,自变量x的取值范围是( )
| A. | x>5 | B. | x≥5 | C. | x≠5 | D. | x<5 |
 如图是我国古代某种铜钱的平面示意图,该图形是在一个圆形的中间挖去一个正方形得到的.若圆的半径是3cm,正方形的边长为xcm,设该图形的面积为ycm2.(注:π取3)
如图是我国古代某种铜钱的平面示意图,该图形是在一个圆形的中间挖去一个正方形得到的.若圆的半径是3cm,正方形的边长为xcm,设该图形的面积为ycm2.(注:π取3)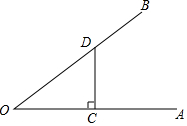 如图,OA、OB是两条射线,点C、D分别在OA、OB上,CD⊥OA,垂足为点C,OC=4,OD=5,若⊙P与OA、OB、CD都相切,则⊙P的半径是1或2.
如图,OA、OB是两条射线,点C、D分别在OA、OB上,CD⊥OA,垂足为点C,OC=4,OD=5,若⊙P与OA、OB、CD都相切,则⊙P的半径是1或2.