题目内容
6.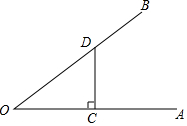 如图,OA、OB是两条射线,点C、D分别在OA、OB上,CD⊥OA,垂足为点C,OC=4,OD=5,若⊙P与OA、OB、CD都相切,则⊙P的半径是1或2.
如图,OA、OB是两条射线,点C、D分别在OA、OB上,CD⊥OA,垂足为点C,OC=4,OD=5,若⊙P与OA、OB、CD都相切,则⊙P的半径是1或2.
分析 分两种情形分别求解即可:①如图当⊙P在△ODC内部时,②当⊙P′在△ODC外部时.
解答 解:如图当⊙P在△ODC内部时,设切点分别为E、F、T,连接PE、PF、PT.则四边形PFCT是正方形.
在Rt△ODC中,∵OC=4,OD=5,
∴CD=$\sqrt{O{D}^{2}-O{C}^{2}}$=3.
易知内切圆半径=$\frac{OC+CD-OD}{2}$=1,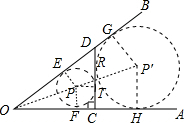
当⊙P′在△ODC外部时,设切点分别为G、R、H.
∵DG=DR,CR=CH,OG=OH,
OG+OH=OD+OC+CD=12,
∴OG=6,
∵tan∠EOP=$\frac{EP}{OE}$=$\frac{GP′}{OG}$,
∴$\frac{1}{3}$=$\frac{GP′}{6}$,
∴GP′=2.
综上所述,⊙P的半径为1或2.
点评 本题考查切线的性质、勾股定理、切线长定理等知识,解题的关键是学会用分类讨论的思想思考问题,则有中考填空题中的压轴题.

练习册系列答案
相关题目
16.-5的倒数的相反数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | -5 | D. | $-\frac{1}{5}$ |
1.下列图形中,不是轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图直线a∥b,PM⊥c,若∠1=50°,则∠2=40°.
如图直线a∥b,PM⊥c,若∠1=50°,则∠2=40°. 如图,有分别过A、B两个加油站的公路l1、l2相交于点O,现准备在∠A0B内部建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且点P到两条公路l1、l2的距离也相等.请用尺规作图作出点P.(不写作法,保留作图痕迹)
如图,有分别过A、B两个加油站的公路l1、l2相交于点O,现准备在∠A0B内部建一个油库,要求油库的位置点P满足到A、B两个加油站的距离相等,而且点P到两条公路l1、l2的距离也相等.请用尺规作图作出点P.(不写作法,保留作图痕迹)