题目内容
12.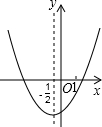 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有以下结论①abc>0;②a+b=0;③a+c<b;④4a+c<2b;⑤2a+c>0,其中正确结论的个数为( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有以下结论①abc>0;②a+b=0;③a+c<b;④4a+c<2b;⑤2a+c>0,其中正确结论的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据二次函数的图象,开口向上说明a>0,与y轴交与负半轴,说明c<0,对称轴-$\frac{b}{2a}$=-$\frac{1}{2}$<0,根据这些条件就可以判断题目中的结论正确与否.
解答 解:由函数图象可知:开口向上,则a>0,与y轴交与负半轴,则c<0,$-\frac{b}{2a}$=-$\frac{1}{2}$<0,知a=b>0,故abc<0,故①错误;因为a=b>0,故a+b>0,故②错误;由图象知,x=1,则y=a+b+c<0,a+c<-b<b,故③正确;由图象知,x=1,则y=a+b+c<0,因为a=b,所以2a+c<0,则4a+c<2a,即4a+c<2b,故④正确,⑤错误.故正确个数为2,故选项A正确,选项B错误,选项C错误,选项D错误.
故选A
点评 本题考察学生对二次函数图象与系数之间的关系的理解,通过图象得到a、b、c的符号,通过对图象观察和灵活变化,得到结论中的各个式子,根据推导判断题目中结论的是否正确.

练习册系列答案
相关题目
4.下列二次函数的图象与x轴有两个交点的是( )
| A. | y=-x2-6x+9 | B. | y=2x2-x+1 | C. | y=-x2+2x-5 | D. | y=2x2-4x+1 |
 己知如图,在梯形ABCD中,AB∥CD.AC、BD为对角线,MN∥CB.且与AB、DC分别相交于点M、N.与DB、AC分别相交于点P、Q.
己知如图,在梯形ABCD中,AB∥CD.AC、BD为对角线,MN∥CB.且与AB、DC分别相交于点M、N.与DB、AC分别相交于点P、Q.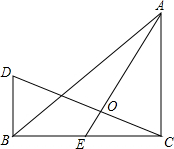 如图,在△ABC中,∠ACB=90°,AC=BC,DB⊥BC于点B,点E在BC上,AE、CD相交于点O,当AE与CD满足怎样的数量关系时,AE⊥CD,并说明理由.
如图,在△ABC中,∠ACB=90°,AC=BC,DB⊥BC于点B,点E在BC上,AE、CD相交于点O,当AE与CD满足怎样的数量关系时,AE⊥CD,并说明理由.