题目内容
4．下列二次函数的图象与x轴有两个交点的是（ ）| A． | y=-x2-6x+9 | B． | y=2x2-x+1 | C． | y=-x2+2x-5 | D． | y=2x2-4x+1 |
分析 计算每个函数的判别式△=b2-4ac，判断△与0的大小关系即可．
解答 解：A、△=（-6）2+4×9=36-26=0，则图象与x轴有一个交点，选项错误；
B、△=（-1）2-4×2×1=1-8=-7＜0，则图象与x轴没有交点，选项错误；
C、△=22-4×（-1）×（-5）=4-20=-16＜0，则图象与x轴没有交点，选项错误；
D、△=（-4）2-4×2×1=16-8=8＞0，则图象与x轴有两个交点，选项正确．
故选D．
点评 本题考查了二次函数与x轴的交点的个数，当△＞0时有两个交点，当△=0时有一个交点，当△＜0时没有交点．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
化简并求值：3（x2-2xy）-[（-$\frac{1}{2}$xy+y2）+（x2-2y2）]，其中x，y的值见数轴表示：
12．
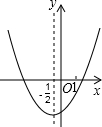已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有以下结论①abc＞0；②a+b=0；③a+c＜b；④4a+c＜2b；⑤2a+c＞0，其中正确结论的个数为（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有以下结论①abc＞0；②a+b=0；③a+c＜b；④4a+c＜2b；⑤2a+c＞0，其中正确结论的个数为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
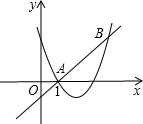如图，直线y=x+m和抛物线y=x2+bx+c都经过点A（1，0），B，且当x=4时，二次函数的值为6．
如图所示，E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为点C，D．求证：