题目内容
20.如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为10cm,最大张角α为150°,你能否利用此圆规,画出一个半径为18cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)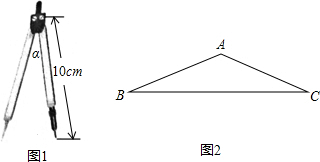
分析 先根据等腰三角形的性质求出∠B的度数,过点A作AD⊥BC于点D,根据锐角三角函数的定义可求出BD的长,故可得出结论.
解答  解:能画出一个半径为18cm的圆.理由如下:
解:能画出一个半径为18cm的圆.理由如下:
∵在△ABC中,AB=AC,∠BAC=150°,
∴∠B=∠C=15°,BC=2BD.
过A作AD⊥BC,垂足为D.
∵在Rt△ABD中,cosB=$\frac{BD}{AB}$,
∴BD=AB•cosB≈10×0.97=9.7,
∴BC=2BD=19.4.
∵19.4>18,
∴能画出一个半径为18cm的圆.
点评 本题考查的是解直角三角形的应用,等腰三角形的性质,熟知锐角三角函数的定义是解答此题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
10.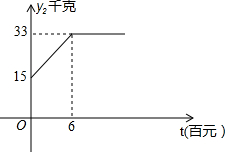 茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).
茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).
(1)试求张大爷每亩丘陵地投资600元和每亩山地投资600元时茶叶的总产量分别是多少千克?
(2)写出张大爷家茶叶总产量W (千克)与丘陵地每亩投资x(百元)之间的函数关系式,并指出x的取值范围;
(3)当x取何值时,茶叶的总产量最高?最高产量为多少千克?
(4)在(2)的条件下,如果其中700千克为毛尖茶.其余为龙井茶.现在由乡政府统一组织向外销售,且包装要求及价格如表:
应如何安排包装,利润最大?最大利润为多少?(利润=销售总价格-总投资资金)
 茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).
茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).(1)试求张大爷每亩丘陵地投资600元和每亩山地投资600元时茶叶的总产量分别是多少千克?
(2)写出张大爷家茶叶总产量W (千克)与丘陵地每亩投资x(百元)之间的函数关系式,并指出x的取值范围;
(3)当x取何值时,茶叶的总产量最高?最高产量为多少千克?
(4)在(2)的条件下,如果其中700千克为毛尖茶.其余为龙井茶.现在由乡政府统一组织向外销售,且包装要求及价格如表:
| 型号 | A型包装 | B型包装 | C型包装 |
| 每盒装 | 龙井1千克 | 毛尖1千克 | 毛尖0.4千克;龙井0.6千克 |
| 每盒价格 | 45元 | 60元 | 56元 |
12.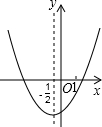 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有以下结论①abc>0;②a+b=0;③a+c<b;④4a+c<2b;⑤2a+c>0,其中正确结论的个数为( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有以下结论①abc>0;②a+b=0;③a+c<b;④4a+c<2b;⑤2a+c>0,其中正确结论的个数为( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有以下结论①abc>0;②a+b=0;③a+c<b;④4a+c<2b;⑤2a+c>0,其中正确结论的个数为( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有以下结论①abc>0;②a+b=0;③a+c<b;④4a+c<2b;⑤2a+c>0,其中正确结论的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
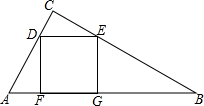 如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积.
如图,已知△ABC中,四边形DEGF为正方形,D、E在线段AC、BC上,F、G在AB上,如果S△ADF=S△CDE=1,S△BEG=3,求△ABC的面积. 化简并求值:3(x2-2xy)-[(-$\frac{1}{2}$xy+y2)+(x2-2y2)],其中x,y的值见数轴表示:
化简并求值:3(x2-2xy)-[(-$\frac{1}{2}$xy+y2)+(x2-2y2)],其中x,y的值见数轴表示: 如图,已知点D、E、F分别在△ABC的边AB、AC、BC上,DE∥BC、DF∥AC,AE=6,EC=8,求BF:FC的值.
如图,已知点D、E、F分别在△ABC的边AB、AC、BC上,DE∥BC、DF∥AC,AE=6,EC=8,求BF:FC的值.