题目内容
5.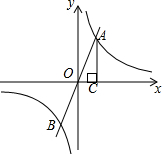 如图,已知点A(x,y)为反比例函数y=$\frac{k}{x}$(k>0)图象位于第一象限上一点,射线AO交双曲线y=$\frac{k}{x}$的另一支于点B,过点A作AC⊥x轴,连接BC.当点A的横坐标x逐渐增大时,则△ABC的面积( )
如图,已知点A(x,y)为反比例函数y=$\frac{k}{x}$(k>0)图象位于第一象限上一点,射线AO交双曲线y=$\frac{k}{x}$的另一支于点B,过点A作AC⊥x轴,连接BC.当点A的横坐标x逐渐增大时,则△ABC的面积( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 不变 | D. | 不确定 |
分析 根据题意,A、B两点关于原点对称,从而得出S△AOC=S△BOC,再根据反比例函数系数k的几何意义作答即可.
解答 解:由题意可知A、B两点关于原点对称,
∴B(-x,-y),
∴S△AOC=S△BOC,
∵S△AOC=$\frac{1}{2}$k,
∴△ABC的面积=S△AOC+S△BOC=2S△AOC=k,
故△ABC的面积是定值k,
故选C.
点评 主要考查了反比例函数 y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
16.假定鸡蛋孵化后,鸡雏为雌或雄的羝概率相同,如果两个鸡蛋全部成功孵化,则两只鸡雏均为雄鸡的槪率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
17.庐阳区是合肥市政治、经济、文化、金融中心,常住人口62.5万,其中数字62.5万用科学记数法表示为( )
| A. | 62.5×104 | B. | 62.5×105 | C. | 6.25×106 | D. | 6.25×105 |
14.如果两圆的半径分别为2cm和5cm,圆心距为6cm,那么这两个圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
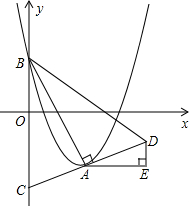 如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.