题目内容
8.先化简,再求值:$\frac{a}{a+2}$-$\frac{1}{a-1}$÷$\frac{a+2}{{a}^{2}-2a+1}$,其中a=sin60°tan30°.分析 先根据分式混合运算的法则把原式进行化简,再求出a的值代入进行计算即可.
解答 解:原式=$\frac{a}{a+2}$-$\frac{1}{a-1}$•$\frac{(a-1)^{2}}{a+2}$
=$\frac{a}{a+2}$-$\frac{a-1}{a+2}$
=$\frac{1}{a+2}$,
当a=sin60°tan30°=$\frac{\sqrt{3}}{2}$•$\frac{\sqrt{3}}{3}$=$\frac{1}{2}$时,原式=$\frac{1}{\frac{1}{2}+2}$=$\frac{2}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
18.2014年12月10日,连通杭州、南昌、长沙三座省会城市的杭长高铁开通,这给勇于创业的衢州人民的出行带来了极大的方便.杭长高铁总投资1300亿元,1300亿元用科学记数法表示为( )
| A. | 13×1010元 | B. | 1.3×1010元 | C. | 0.13×1012元 | D. | 1.3×1011元 |
16.假定鸡蛋孵化后,鸡雏为雌或雄的羝概率相同,如果两个鸡蛋全部成功孵化,则两只鸡雏均为雄鸡的槪率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
17.庐阳区是合肥市政治、经济、文化、金融中心,常住人口62.5万,其中数字62.5万用科学记数法表示为( )
| A. | 62.5×104 | B. | 62.5×105 | C. | 6.25×106 | D. | 6.25×105 |
 如图,在等腰△ABC中,∠ABC=90°,D为AC边的中点,过D作DE⊥DF,交AB于E,交BC于F,BC=7,CF=3,求EF的长.
如图,在等腰△ABC中,∠ABC=90°,D为AC边的中点,过D作DE⊥DF,交AB于E,交BC于F,BC=7,CF=3,求EF的长.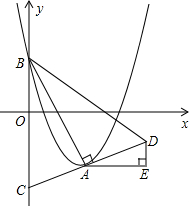 如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.
如图,在平面直角坐标系xOy中,抛物线y=(x-m)2-m2+m的顶点为A,与y轴的交点为B,连结AB,AC⊥AB,交y轴于点C,延长CA到点D,使AD=AC,连结BD.作AE∥x轴,DE∥y轴.