题目内容
6.在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{AE}{EC}$=$\frac{2}{3}$.分析 根据平行线分线段成比例定理即可得.
解答 解:∵DE∥BC,
∴$\frac{AE}{EC}$=$\frac{AD}{DB}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题主要考查平行线分线段成比例,掌握平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例是解题的关键.

练习册系列答案
相关题目
16.若$\sqrt{{(2a+4)}^{2}}$=2a+4,则a的取值范围为( )
| A. | a≥2 | B. | a≤2 | C. | a≥-2 | D. | a≤-2 |
1.平面上有2004条直线,且任何两条不平行,任何三条不共点,则它们彼此相交而成的线段有( )
| A. | 2003×2002×1002 | B. | 2003×2002×2004 | C. | 2004×2003×1002 | D. | 2004×2003×2004 |
16.下列运算正确的是( )
| A. | 2a2•3a2=6a2 | B. | (-2ab)(3a2b+2ab2)=-6a3b2+4a2b3 | ||
| C. | (a+3b)2=a2+3ab+9b2 | D. | (3a+b)(a-2b)=3a2-5ab-2b2 |
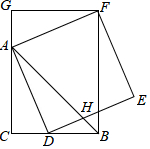 如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,以AD为边作正方形ADEF,过点F作FG⊥CA交CA的延长线于点G,连接FB交DE于点H,下列结论:
如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,以AD为边作正方形ADEF,过点F作FG⊥CA交CA的延长线于点G,连接FB交DE于点H,下列结论: