题目内容
3．某商场将每件进价为80元的某种商品原来按每件100出售，一天可售出100件，后来经过市场调查，发现这种商品每降低1元，其销量可增加10件．（1）求商场经营该商品原来一天可获利润多少元？
（2）设后来该商品每件降价x元，若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？
分析 （1）原来一天可获利润=（原售价-原进价）×一天的销售量；
（2）设每件商品应降价x元，等量关系为：降价后的单件利润×销售量=总利润，依此列方程解答．
解答 解：（1）（100-80）×100=2000（元），
答：商场经营该商品原来一天可获利润2000元；
（2）设每件商品应降价x元，依题意得：
（100-80-x）（100+10x）=2160，
即x2-10x+16=0，
解得：x1=2，x2=8．
答：每件商品应降价2元或8元．
点评 此题考查一元二次方程的实际运用，掌握销售问题中的基本数量关系是解决问题的关键．
练习册系列答案
相关题目
13．
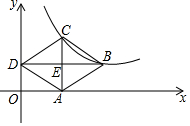如图，菱形ABCD的顶点A在x轴上，D在y轴上，B、C在反比例函数的图象上，对角线AC、BD交于点E，且BD∥x轴，若AE=1，∠ADE=30°，则反比例函数的表达式为（ ）
如图，菱形ABCD的顶点A在x轴上，D在y轴上，B、C在反比例函数的图象上，对角线AC、BD交于点E，且BD∥x轴，若AE=1，∠ADE=30°，则反比例函数的表达式为（ ）| A． | $y=\frac{2}{x}$ | B． | $y=\frac{3}{x}$ | C． | $y=\frac{{\sqrt{3}}}{x}$ | D． | $y=\frac{{2\sqrt{3}}}{x}$ |
12．在五张完全相同的卡片上，分别写有数字-2，-1，0，1，2，现从中随机抽取一张，抽到写有正数的卡片的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |