题目内容
13.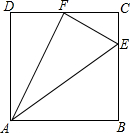 如图,正方形ABCD中,E、F分别是BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=FD,连接AE、EF、AF,你能找出图中所有的相似三角形吗?试说明理由.
如图,正方形ABCD中,E、F分别是BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=FD,连接AE、EF、AF,你能找出图中所有的相似三角形吗?试说明理由.
分析 设正方形的边长为4x,根据题意求出三角形的边长,根据相似三角形的判定定理证明即可.
解答 解:△ECF∽△FDA;△EFA∽△FDA;△EFA∽△ECF.
∵$\frac{CE}{BE}$=$\frac{1}{3}$,∴BC=4CE,
设正方形的边长为4x,则CE=x,CF=2x,
由勾股定理得,EF=$\sqrt{5}$x,AF=2$\sqrt{5}$x,AE=5x,
∴$\frac{CE}{DF}$=$\frac{CF}{AD}$=$\frac{1}{2}$,∠C=∠D=90°,
∴△ECF∽△FDA;
∵$\frac{EF}{DF}$=$\frac{AF}{AD}$$\frac{AE}{AF}$=$\frac{\sqrt{5}}{2}$,
∴△EFA∽△FDA;
∴△EFA∽△ECF.
点评 本题考查的是相似三角形的判定,掌握两边对应成比例、夹角相等的两个三角形相似和三边对应成比例的两个三角形相似是解题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
1.若|a|=5,|b|=$\frac{1}{5}$,则a÷b×$\frac{1}{b}$等于( )
| A. | ±5 | B. | ±25 | C. | ±125 | D. | -25或-5 |
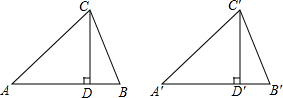 如图,已知在△ABC和△A′B′C′中,CD,C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.求证:△ABC≌△A′B′C′.
如图,已知在△ABC和△A′B′C′中,CD,C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.求证:△ABC≌△A′B′C′.
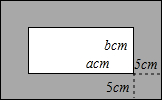 长方形壁画的长为a cm,宽为b cm,现要在其四周镶上宽为5cm的彩条(如图),至少需要多长的彩条才能镶完?所列的式子是否是整式?若是整式,请判断它是单项式还是多项式.
长方形壁画的长为a cm,宽为b cm,现要在其四周镶上宽为5cm的彩条(如图),至少需要多长的彩条才能镶完?所列的式子是否是整式?若是整式,请判断它是单项式还是多项式.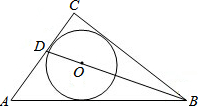 如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交BC于D,若BD=10,CD=6,则⊙O半径为$\frac{24}{7}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交BC于D,若BD=10,CD=6,则⊙O半径为$\frac{24}{7}$.