题目内容
8.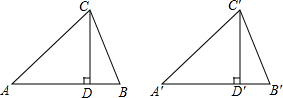 如图,已知在△ABC和△A′B′C′中,CD,C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.求证:△ABC≌△A′B′C′.
如图,已知在△ABC和△A′B′C′中,CD,C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.求证:△ABC≌△A′B′C′.
分析 根据HL,可得Rt△ACD≌Rt△A′C′D′,再根据ASA,可得答案.
解答 证明:在Rt△ACD和Rt△A′C′D′中,
$\left\{\begin{array}{l}{AC=A′C′}\\{CD=C′D′}\end{array}\right.$,
∴Rt△ACD≌Rt△A′C′D′(HL),
∴∠CAD=∠C′A′D′.
在△ABC和△A′B′C′中,
$\left\{\begin{array}{l}{∠BAC=∠B′A′C′}\\{AC=A′C′}\\{∠ACB=∠A′C′B′}\end{array}\right.$,
∴△ABC≌△A′B′C′(ASA).
点评 本题考查了全等三角形的判定,利用了“HL“,“ASA“正明三角形全等.

练习册系列答案
相关题目
 如图,已知$\frac{AB}{BE}=\frac{AD}{DE}=\frac{AC}{CE}$,求证:$\frac{AB+BC+CA}{BC}=\frac{AE}{DE}$.
如图,已知$\frac{AB}{BE}=\frac{AD}{DE}=\frac{AC}{CE}$,求证:$\frac{AB+BC+CA}{BC}=\frac{AE}{DE}$.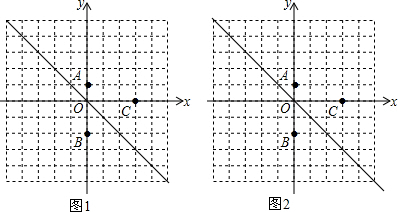
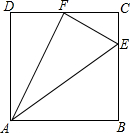 如图,正方形ABCD中,E、F分别是BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=FD,连接AE、EF、AF,你能找出图中所有的相似三角形吗?试说明理由.
如图,正方形ABCD中,E、F分别是BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=FD,连接AE、EF、AF,你能找出图中所有的相似三角形吗?试说明理由.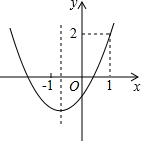 已知抛物线y=ax2+bx+c的图象如图所示.
已知抛物线y=ax2+bx+c的图象如图所示.