题目内容
1.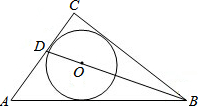 如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交BC于D,若BD=10,CD=6,则⊙O半径为$\frac{24}{7}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交BC于D,若BD=10,CD=6,则⊙O半径为$\frac{24}{7}$.
分析 连接OE,根据切线的性质得到OE⊥BC,得到OE∥CD,根据平行线分线段成比例定理得到$\frac{BO}{BD}$=$\frac{OE}{CD}$,代入数据计算即可.
解答 解: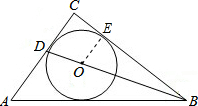 连接OE,
连接OE,
设⊙O半径为R,
∵∠C=90°,BD=10,CD=6,
∴BC=$\sqrt{B{D}^{2}-C{D}^{2}}$=8
∵BC与⊙O相切于E,
∴OE⊥BC,又∠C=90°,
∴OE∥CD,
∴$\frac{BE}{BC}$=$\frac{OE}{CD}$,即$\frac{8-R}{8}$=$\frac{R}{6}$,
解得,R=$\frac{24}{7}$,
故答案为:$\frac{24}{7}$.
点评 本题考查的是三角形的内切圆和内心的知识,掌握圆的切线垂直于过切点的半径、正确运用平行线分线段成比例定理是解题的关键.

练习册系列答案
相关题目
10.如图1所示,E、F分别为透明正方体的面ADD1A1,面BCC1B1的中心,则四边形BFD1E的正视图、左视图、俯视图分别是图2中的( )
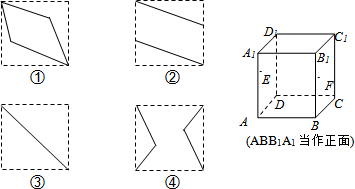

| A. | ②③② | B. | ①②① | C. | ①②③ | D. | ②③④ |
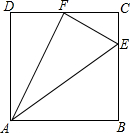 如图,正方形ABCD中,E、F分别是BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=FD,连接AE、EF、AF,你能找出图中所有的相似三角形吗?试说明理由.
如图,正方形ABCD中,E、F分别是BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=FD,连接AE、EF、AF,你能找出图中所有的相似三角形吗?试说明理由.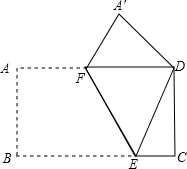 如图,将矩形ABCD沿折痕FE对折,使点B与点D重合,点A落在点A′.
如图,将矩形ABCD沿折痕FE对折,使点B与点D重合,点A落在点A′.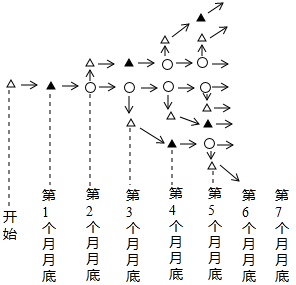 如果用△表示一对新出生的小兔,用▲表示一对一个月大的成年兔子,用○表示一对能生小兔的成年兔子,请你在图中标出第6个月月底和第7个月月底的各对兔子,把这幅图补充完整.
如果用△表示一对新出生的小兔,用▲表示一对一个月大的成年兔子,用○表示一对能生小兔的成年兔子,请你在图中标出第6个月月底和第7个月月底的各对兔子,把这幅图补充完整.