��Ŀ����
��֪����ͼ�����ı���OABC�У�AB��OC��BC��x���ڵ�C��A��1����1����B��3����1��������P�ӵ�O����������x����������ÿ��2����λ���ȵ��ٶ��ƶ�������P��PQ��ֱ��ֱ��OA������Ϊ��Q�����P�ƶ���ʱ��t�루0��t��2������OPQ���ı���OABC�ص����ֵ����ΪS��
��1����O��A��B����������ߵĽ���ʽ��
��2���������OPQ���ŵ�P����ʱ�뷽����ת90�㣬�Ƿ����t��ʹ�á�OPQ�Ķ���O��Q���������ϣ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��3�����S��t�ĺ�����ϵʽ��


��
�����㡿���κ����ۺ��⣮
����������1���������߽���ʽΪy=ax2+bx��a��0����Ȼ��ѵ�A��B������������a��b��ֵ�����ɵý⣻
��2��������ת�����������O��Q�����꣬Ȼ��ֱ���������߽���ʽ����⼴�ɣ�
��3�������Q���A�غ�ʱ��t=1����P���C�غ�ʱ��t=1.5��t=2ʱPQ������B��Ȼ��֢�0��t��1ʱ���ص����ֵ�������ڡ�POQ���������1��t��1.5ʱ���ص����ֵ����������������ֱ�������ε�����IJ��1.5��t��2ʱ���ص����ֵ�����������ε������ȥһ������ֱ�������ε�����ֱ���ʽ�������ɵý⣮
����𡿽⣺��1���������߽���ʽΪy=ax2+bx��a��0����
�ѵ�A��1����1����B��3����1������ã�
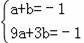
 ��
��
��ã�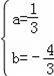
 ��
��
�������߽���ʽΪy=
 x2��
x2��
 x��
x��
��2����ͼ1���ߵ�P�ӵ�O�����ٶ���ÿ��2����λ���ȣ�
��OP=2t��
���P��������2t��0����
��A��1����1����
���AOC=45�㣬
���Q��x�ᡢy��ľ��붼��
 OP=
OP=
 ��2t=t��
��2t=t��
���Q��������t����t����
�ߡ�OPQ���ŵ�P����ʱ�뷽����ת90�㣬
����ת���O��Q�Ķ�Ӧ�������ֱ�Ϊ��2t����2t������3t����t����
������O���������ϣ���
 ����2t��2��
����2t��2��
 ����2t��=��2t��
����2t��=��2t��
��ã�t=
 ��
��
������Q���������ϣ���
 ����3t��2��
����3t��2��
 ����3t��=��t��
����3t��=��t��
��ã�t=1��
��������������t=
 ��1��ʹ�á�OPQ�Ķ���O��Q���������ϣ�
��1��ʹ�á�OPQ�Ķ���O��Q���������ϣ�
��3����ͼ2����Q���A�غ�ʱ��OP=1��2=2��t=2��2=1��
��P���C�غ�ʱ��OP=3��t=3��2=1.5��
t=2ʱ��OP=2��2=4��PC=4��3=1����ʱPQ������B��
���ԣ�������������ۣ�
��0��t��1ʱ���ص����ֵ�������ڡ�POQ�������S=
 ����2t����
����2t����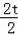
 =t2��
=t2��
��1��t��1.5ʱ���ص����ֵ����������������ֱ�������ε�����IJ
S=
 ����2t����
����2t����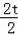
 ��
��
 ����
����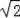
 t��
t��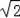
 ��2=2t��1��
��2=2t��1��
��1.5��t��2ʱ���ص����ֵ�����������ε������ȥһ������ֱ�������ε����
S=
 ����2+3����1��
����2+3����1��
 ��[1����2t��3��]2=��2��t��2��2+
��[1����2t��3��]2=��2��t��2��2+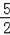
 ��
��
���ԣ�S��t�Ĺ�ϵʽΪS=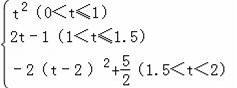
 ��
��
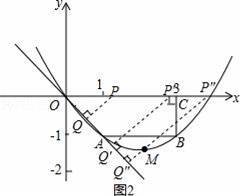



��������������Ҫ�����˶��κ����ۺ����ͣ���Ҫ�����˴���ϵ��������κ�������ʽ������ֱ�������ε����ʣ����κ���ͼ���ϵ�����������������ε�������ѵ����ڣ�3�������˶�ʱ��ı仯�������ص����ֵ���״�IJ�ͬ��������ۣ�����ͼ�θ�����ֱ�ۣ�
����

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
 ��ͼ����ͼ��ʾ�����½�����ȷ���ǣ�������
��ͼ����ͼ��ʾ�����½�����ȷ���ǣ�������



 =2�Ľ��ǣ�������
=2�Ľ��ǣ�������




 ��B.
��B. ��C.��
��C.�� D.
D.  ��
��