题目内容
分解因式: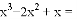 ______________.
______________.
 .
【解析】试题分析:==.故答案为:.
.
【解析】试题分析:==.故答案为:.
练习册系列答案
相关题目
某中学初中生在做练习册作业上解一个一元一次不等式时,发现不等式右边的一个数被墨迹污染看不清了,所看到的不等式是1-3x<▇,他查看练习本后的答案知道,这个不等式的解集是x>5,那么被污染的数是 __________ .
 -14
【解析】设被污染的数为a,不等式为1-3x<a,解得:x>,由已知解集为x>5,得到=5解得:a=-14.
故答案为:-14
-14
【解析】设被污染的数为a,不等式为1-3x<a,解得:x>,由已知解集为x>5,得到=5解得:a=-14.
故答案为:-14 ______
 【解析】根据整式乘法和因式分解的互逆性,可知3x(x+1)=3x2+x.
故答案为:3x2+x.
【解析】根据整式乘法和因式分解的互逆性,可知3x(x+1)=3x2+x.
故答案为:3x2+x. 如果多项式x2-kx+9能用公式法分解因式,则k的值是多少?
 k=±6
【解析】试题分析:根据题意判断出题目中的多项式为完全平方式,然后可根据完全平方式计算即可.
试题解析:∵多项式x2-kx+9能用公式法分解因式,并且它有三项,
∴它是一个完全平方式,
∴这两个数是3、x,
∴k=±2×3=±6
k=±6
【解析】试题分析:根据题意判断出题目中的多项式为完全平方式,然后可根据完全平方式计算即可.
试题解析:∵多项式x2-kx+9能用公式法分解因式,并且它有三项,
∴它是一个完全平方式,
∴这两个数是3、x,
∴k=±2×3=±6 因式分解: 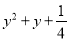 =______
=______
 【解析】根据完全平方公式进行因式分解为: .
故答案为:
.
【解析】根据完全平方公式进行因式分解为: .
故答案为:
. 如果多项式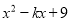 能用公式法分解因式,那么k的值是( )
能用公式法分解因式,那么k的值是( )
A. 3 B. 6 C. 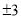 D.
D. 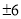
 D
【解析】由于可以利用公式法分解因式,所以它是一个完全平方式,所以.
故选:D.
D
【解析】由于可以利用公式法分解因式,所以它是一个完全平方式,所以.
故选:D. 如图,已知AB=AC,E,D分别是AB,AC的中点,且AF⊥BD交BD的延长线于F,AG⊥CE交CE的延长线于G,试判断AF和AG的关系是否相等,并说明理由.
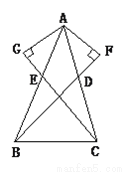
 AF=AG
【解析】试题分析:先由SAS证得△ABD≌△ACE,由全等三角形对应边相等得∠ABD=∠ACE,由AAS证得△ABF≌△ACG,即可证得AF=AG.
试题解析:
∵AB=AC,E,D分别是AB,AC的中点,
∴ AD=AE.
∴在△ABD和△ACE中,
∴△ABD≌△ACE (SAS).
∴∠ABD=∠ACE,
在△ABF和△ACG中,
...
AF=AG
【解析】试题分析:先由SAS证得△ABD≌△ACE,由全等三角形对应边相等得∠ABD=∠ACE,由AAS证得△ABF≌△ACG,即可证得AF=AG.
试题解析:
∵AB=AC,E,D分别是AB,AC的中点,
∴ AD=AE.
∴在△ABD和△ACE中,
∴△ABD≌△ACE (SAS).
∴∠ABD=∠ACE,
在△ABF和△ACG中,
... 在下列条件中,不能说明△ABC≌△A’B’C’的是( )
A. ∠A=∠A’,∠C=∠C’,AC=A’C’ B. ∠A=∠A’,AB=A’B’,BC=B’C’
C. ∠B=∠B’,∠C=∠C’,AB=A’B’ D. AB=A’B’, BC=B’ C’AC=A’C’
 B
【解析】A、∠A=∠A′,∠C=∠C′,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确;
B、∠A=∠A′,AB=A′B′,BC=B′C′,SSA不能判定两个三角形全等,故选项错误;
C、∠B=∠B′,∠C=∠C′,AB=A′B′,可用AAS判定△ABC≌△A′B′C,故选项正确;
D、AB=A′B′,BC=B′C,AC=A′C′,可用ASA判定△AB...
B
【解析】A、∠A=∠A′,∠C=∠C′,AC=A′C′,可用ASA判定△ABC≌△A′B′C,故选项正确;
B、∠A=∠A′,AB=A′B′,BC=B′C′,SSA不能判定两个三角形全等,故选项错误;
C、∠B=∠B′,∠C=∠C′,AB=A′B′,可用AAS判定△ABC≌△A′B′C,故选项正确;
D、AB=A′B′,BC=B′C,AC=A′C′,可用ASA判定△AB... 如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角.若∠A=120°,则∠1+∠2+∠3+∠4= .

 300°
【解析】由题意得,∠5=180°-∠EAB=60°
,
又∵多边形的外角和为360°,
∴∠1+∠2+∠3+∠4=360°-∠5=300°.
300°
【解析】由题意得,∠5=180°-∠EAB=60°
,
又∵多边形的外角和为360°,
∴∠1+∠2+∠3+∠4=360°-∠5=300°. 
