题目内容
15.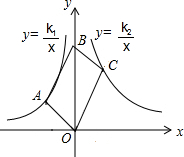 如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )
如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )| A. | -2k1 | B. | 2k2 | C. | k1+k2 | D. | k2-k1 |
分析 先过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,再根据反比例函数系数k的几何意义,求得△ABE的面积=△COD的面积相等=$\frac{1}{2}$|k2|,△AOE的面积=△CBD的面积相等=$\frac{1}{2}$|k1|,最后计算平行四边形OABC的面积.
解答 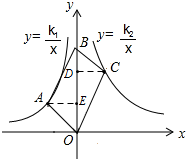 解:过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,
解:过点A作AE⊥y轴于点E,过点C作CD⊥y轴于点D,
根据∠AEB=∠CD0=90°,∠ABE=∠COD,AB=CO可得:△ABE≌△COD(AAS),
∴△ABE与△COD的面积相等,
又∵点C在y=$\frac{{k}_{2}}{x}$的图象上,
∴△ABE的面积=△COD的面积相等=$\frac{1}{2}$|k2|,
同理可得:△AOE的面积=△CBD的面积相等=$\frac{1}{2}$|k1|,
∴平行四边形OABC的面积=2($\frac{1}{2}$|k2|+$\frac{1}{2}$|k1|)=|k2|+|k1|=k2-k1,
故选:D.
点评 本题主要考查了反比例函数系数k的几何意义,在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
10.在直角坐标系中,点(-2,1)关于原点的对称点是( )
| A. | (2,-1) | B. | (1,2) | C. | (-2,-1) | D. | (-1,2) |
20. 如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )
如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )
 如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )
如图,∠1=∠2是对顶角,∠1=180°-α,∠2=35°,则α的度数是( )| A. | 155° | B. | 35° | C. | 135° | D. | 145° |
4.数据0,1,2,x,3的平均数是2,则x的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 如图,在直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).
如图,在直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).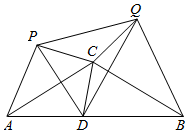 如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
