题目内容
7.如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PA•PC,连接CE,AE,OE,OE交CA于点D.
(1)求证:△PAE∽△PEC;
(2)求证:PE为⊙O的切线;
(3)若∠B=30°,AP=$\frac{1}{2}$AC,求证:DO=DP.
分析 (1)利用两边对应成比例,夹角相等,两三角形相似即可;
(2)连接BE,转化出∠OEB=∠PCE,又由相似得出∠PEA=∠PCE,从而用直径所对的圆周角是直角,转化出∠OEP=90°即可;
(3)构造全等三角形,先找出OD与PA的关系,再用等积式找出PE与PA的关系,从而判断出OM=PE,得出△ODM≌△PDE即可.
解答 解:(1)∵PE2=PA•PC,
∴$\frac{PE}{PA}=\frac{PC}{PE}$,
∵∠APE=∠EPC,
∴△PAE∽△PEC;
(2)如图1,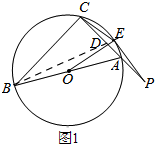
连接BE,
∴∠OBE=∠OEB,
∵∠OBE=∠PCE,
∴∠OEB=∠PCE,
∵△PAE∽△PEC,
∴∠PEA=∠PCE,
∴∠PEA=∠OEB,
∵AB为直径,
∴∠AEB=90°,
∴∠OEB+∠OEA=90°,
∵∠PEA+∠OEA=90°,
∴∠OEP=90°,
∵点E在⊙O上,
∴PE是⊙O的切线;
(3)如图,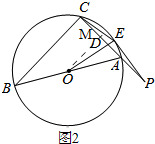
过点O作OM⊥AC于M,
∴AM=$\frac{1}{2}$AC,
∵BC⊥AC,
∴OM∥BC,
∵∠ABC=30°,
∴∠AOM=30°,
∴OM=$\sqrt{3}$AM=$\frac{\sqrt{3}}{2}$AC,
∵AP=$\frac{1}{2}$AC,
∴OM=$\sqrt{3}$AP,
∵PC=AC+AP=2AP+AP=3AP,
∴PE2=PA×PC=PA×3PA,
∴PE=$\sqrt{3}$PA,
∴OM=PE,
∵∠PED=∠OMD=90°,∠ODM=∠PDE,
∴△ODM≌△PDE,
∴OD=DP.
点评 此题是圆的综合题,主要考查了相似三角形的判定和性质,圆的性质,全等三角形的判定和学生,解本题的关键是构造全等三角形,难点是找OD=PE.

练习册系列答案
相关题目
15.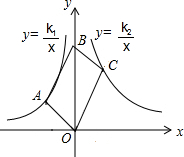 如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )
如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )
 如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )
如图,平行四边形OABC的顶点O,B在y轴上,顶点A在y=$\frac{{k}_{1}}{x}$(k1<0)上,顶点C在y=$\frac{{k}_{2}}{x}$(k2>0)上,则平行四边形OABC的面积是( )| A. | -2k1 | B. | 2k2 | C. | k1+k2 | D. | k2-k1 |
12.下列数2,π,$\frac{22}{7}$,-$\sqrt{2}$,$\sqrt{9}$中,无理数的个数有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.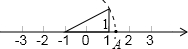 如图所示:数轴上点A所表示的数为a,则a的值是( )
如图所示:数轴上点A所表示的数为a,则a的值是( )
 如图所示:数轴上点A所表示的数为a,则a的值是( )
如图所示:数轴上点A所表示的数为a,则a的值是( )| A. | $\sqrt{5}$+1 | B. | -$\sqrt{5}$+1 | C. | $\sqrt{5}$ | D. | $\sqrt{5}$-1 |
16.下列函数的解析式中是一次函数的是( )
| A. | y=$\frac{1}{-x}$ | B. | y=$\frac{1}{5}$x+1 | C. | y=x2+1 | D. | y=$\sqrt{x}$ |