题目内容
14.解下列方程(组):(1)$\frac{x-1}{3}$-$\frac{x+2}{6}$=1;
(2)$\left\{\begin{array}{l}{a+b+c=2}\\{4a+2b+c=3}\\{a-b+c=6}\end{array}\right.$.
分析 (1)先把方程两边乘以6,再去括号、移项,然后合并即可得到x的值;
(2)$\left\{\begin{array}{l}{a+b+c=2①}\\{4a+2b+c=3②}\\{a-b+c=6③}\end{array}\right.$,先用②-③得3a+b=1④,再用①-③得2b=-4,解得b=-2,然后利用代入法求出a、c的值,从而得到方程组的解.
解答 解:(1)去分母得2(x-1)-(x+2)=6,
去括号得2x-2-x-2=6,
移项得2x-x=6+2+2,
合并得x=10;
(2)$\left\{\begin{array}{l}{a+b+c=2①}\\{4a+2b+c=3②}\\{a-b+c=6③}\end{array}\right.$,
②-③得3a+b=1④,
①-③得2b=-4,解得b=-2,
把b=-2代入④得3a-2=1,解得a=1,
把a=1,b=-2代入①得1-2+c=2,解得c=3,
所以方程组的解为$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=3}\end{array}\right.$.
点评 本题考查了解三元一次不等式组:利用加减消元或代入消元,把解三元一次方程组的问题转化为解二元一次方程组的问题.也考查了解一元一次方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知a,b,c均为实数,且a>b,c≠0,则下列结论不一定正确的是( )
| A. | a+c>b+c | B. | -a<-b | C. | a2>b2 | D. | $\frac{a}{{c}^{2}}$>$\frac{b}{{c}^{2}}$ |
5.某企业今年1月份产值为a万元,2月份比1月份减少了10%,3月份又开始了回暖,已知3,4月份平均月增长率为10%,则4月份的产值是( )
| A. | (a-10%)(a+20%)万元 | B. | a(1-10%)(1+10%)2万元 | ||
| C. | a(1-10%)(1+20%)万元 | D. | a(1+10%)万元 |
6.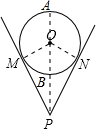 一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )
一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )
 一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )
一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧$\widehat{MN}$的长为( )| A. | $\frac{50}{3}$πcm | B. | 50πcm | C. | $\frac{50}{6}$πcm | D. | 50$\sqrt{3}$πcm |
3.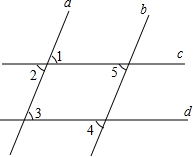 如图所示,则下列说法中不正确的是( )
如图所示,则下列说法中不正确的是( )
 如图所示,则下列说法中不正确的是( )
如图所示,则下列说法中不正确的是( )| A. | 由a∥b能得到∠2=∠5 | B. | 由c∥d能得到∠3=∠1 | ||
| C. | 由c∥d能得到∠3=∠4 | D. | 由a∥b能得到∠1=∠5 |
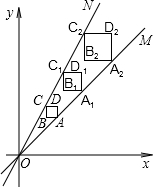 如图,正方形ABCD、正方形A1B1C1D1和正方形A2B2C2D2均位于平面直角坐标系的第一象限内,它们的边平行于x轴或y轴,其中点A,A1,A2在直线OM上,点C,C1,C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.
如图,正方形ABCD、正方形A1B1C1D1和正方形A2B2C2D2均位于平面直角坐标系的第一象限内,它们的边平行于x轴或y轴,其中点A,A1,A2在直线OM上,点C,C1,C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1. 在10×10正方形的网格中,每个正方形的边长均为一个单位,将ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请画出△A′B′C′和△A″B″C′.(不写画法)
在10×10正方形的网格中,每个正方形的边长均为一个单位,将ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请画出△A′B′C′和△A″B″C′.(不写画法)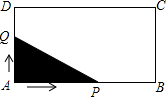 如图,长方形ABCD中,AB=4,AD=2.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是0<x≤$\frac{4}{3}$或x=2.
如图,长方形ABCD中,AB=4,AD=2.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为x(秒),在整个运动过程中,当△APQ为直角三角形时,则相应的x的值或取值范围是0<x≤$\frac{4}{3}$或x=2.