题目内容
4．计算：（1）（$\frac{2}{3}$）-1+（π-3）0+（-2）-2+|（-2）3|
（2）（9x3y-12xy3+3xy2）÷（-3xy）-（2y+x）（2y-x），其中x=1，y=-2．
分析 （1）根据零指数幂、负整数指数幂的运算法则以及绝对值的性质计算即可；
（2）根据多项式除单项式的运算法则以及平方差公式把原式化简，代入计算即可．
解答 解：（1）（$\frac{2}{3}$）-1+（π-3）0+（-2）-2+|（-2）3|
=$\frac{3}{2}$+1+$\frac{1}{4}$+8
=$\frac{43}{4}$；
（2）（9x3y-12xy3+3xy2）÷（-3xy）-（2y+x）（2y-x）
=-3x2+4y2-y-4y2+x2
=-2x2-y，
当x=1，y=-2时，原式=-2×1-（-2）=0．
点评 本题考查的是整式的混合运算，掌握零指数幂、负整数指数幂的运算法则以及多项式除单项式的运算法则是解题的关键．
练习册系列答案
相关题目
14．已知四点A（0，-2），B（1，0），C（2，2），D（0，4），若一个二次函数的图象经过这四点中的三点，则这个二次函数图象的对称轴为（ ）
| A． | x=$\frac{7}{6}$ | B． | x=-$\frac{7}{6}$ | C． | x=-$\frac{6}{7}$ | D． | x=$\frac{6}{7}$ |
15．下列算式能用平方差公式计算的是（ ）
| A． | （-m-n）（-m+n） | B． | $（\frac{1}{2}x+1）（-\frac{1}{2}x-1）$ | C． | （3x-y）（-3x+y） | D． | （2a+b）（2b-a） |
19．
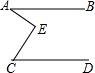如图，已知直线AB∥CD，∠A=20°，∠C=40°，则∠E=（ ）
如图，已知直线AB∥CD，∠A=20°，∠C=40°，则∠E=（ ）| A． | 20° | B． | 40° | C． | 60° | D． | 80° |