题目内容
15.下列算式能用平方差公式计算的是( )| A. | (-m-n)(-m+n) | B. | $(\frac{1}{2}x+1)(-\frac{1}{2}x-1)$ | C. | (3x-y)(-3x+y) | D. | (2a+b)(2b-a) |
分析 可以用平方差公式计算的式子的特点是:两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数.相乘的结果应该是:右边是乘式中两项的平方差(相同项的平方减去相反项的平方).
解答 解:A、(-m-n)(-m+n)=m2-n2符合平方差公式的形式,故正确;
B、原式=-($\frac{1}{2}$x+1)($\frac{1}{2}$x+1)=-($\frac{1}{2}$x+1)2不符合平方差公式的形式,故错误;
C、原式=-(3x-y)(3x-y)=(3x-y)2不符合平方差公式的形式,故错误;
D、原式=(2a+b)(2b-a)=ab-2a2+2b2不符合平方差公式的形式,故错误.
故选A.
点评 本题考查了平方差公式,比较简单,关键是要熟悉平方差公式的结构.公式(a+b)(a-b)=a2-b2.

练习册系列答案
相关题目
5. Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线$y=\frac{k}{x}(k≠0)$经过CD点及AB的中点D,S△BCD=4,则k的值为( )
Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线$y=\frac{k}{x}(k≠0)$经过CD点及AB的中点D,S△BCD=4,则k的值为( )
 Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线$y=\frac{k}{x}(k≠0)$经过CD点及AB的中点D,S△BCD=4,则k的值为( )
Rt△ABC在平面坐标系中摆放如图,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线$y=\frac{k}{x}(k≠0)$经过CD点及AB的中点D,S△BCD=4,则k的值为( )| A. | 8 | B. | -8 | C. | -10 | D. | 10 |
7.如果代数式$\frac{\sqrt{x}}{\sqrt{x-1}}$有意义,那么x的取值范围是( )
| A. | x≥0 | B. | x≠1 | C. | x>1 | D. | x≥0且 x≠1 |
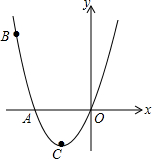 如图,已知抛物线经过点A(-2,0),B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(-2,0),B(-3,3)及原点O,顶点为C. 如图所示,通过平移,△ABC的顶点A移到点D,画出平移后的图形,并找出图中所有平行且相等的线段.
如图所示,通过平移,△ABC的顶点A移到点D,画出平移后的图形,并找出图中所有平行且相等的线段.