题目内容
3.化简:$\frac{a+2\sqrt{ab}+b}{a-b}$-($\frac{\sqrt{a}}{a+\sqrt{ab}}$-$\frac{\sqrt{b}}{b-\sqrt{ab}}$)÷$\frac{\sqrt{b}}{b+\sqrt{ab}}$.分析 先在实数范围能因式分解,约分后,再进一步先把括号内的通分计算,再算除法,最后算减法.
解答 解:原式=$\frac{(\sqrt{a}+\sqrt{b})^{2}}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}$-($\frac{1}{\sqrt{a}+\sqrt{b}}$-$\frac{1}{\sqrt{b}-\sqrt{a}}$)÷$\frac{1}{\sqrt{a}+\sqrt{b}}$
=$\frac{1}{\sqrt{a}-\sqrt{b}}$-(1+$\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}$)
=$\frac{1}{\sqrt{a}-\sqrt{b}}$-$\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}-\sqrt{b}}$-1
=$\frac{\sqrt{a}+\sqrt{b}}{a-b}$-$\frac{a+b+2\sqrt{ab}}{a-b}$-1
=$\frac{\sqrt{a}+\sqrt{b}-2\sqrt{ab}-2a}{a-b}$.
点评 此题考查二次根式的混合运算,根据算式的特点,灵活运用因式分解,二次根式的性质化简.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
13. 如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )
如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )
 如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )
如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
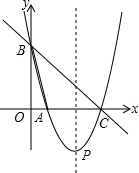 如图,直线y=-x+4与x轴、y轴分别交于点C、B,抛物线y=ax2+bx+c经过点B、C,并与x轴交于另一点A,其顶点为P,tan∠OAB=4.
如图,直线y=-x+4与x轴、y轴分别交于点C、B,抛物线y=ax2+bx+c经过点B、C,并与x轴交于另一点A,其顶点为P,tan∠OAB=4.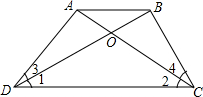 已知,∠1=∠2,∠3=∠4.求证:△ADC≌△BCD.
已知,∠1=∠2,∠3=∠4.求证:△ADC≌△BCD.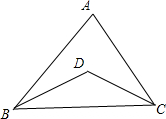 如图,BD,CD分别是△ABC的内角∠ABC、∠ACB的平分线,请说明∠BDC与∠A之间的等量关系是∠BDC=90°+$\frac{1}{2}$∠A.
如图,BD,CD分别是△ABC的内角∠ABC、∠ACB的平分线,请说明∠BDC与∠A之间的等量关系是∠BDC=90°+$\frac{1}{2}$∠A.