题目内容
18．已知a+$\frac{1}{a}$=$\sqrt{10}$，（1）求a2+$\frac{1}{{a}^{2}}$的值；
（2）求a-$\frac{1}{a}$的值．
分析 （1）把已知等式两边平方，利用完全平方公式化简，整理即可求出所求式子的值；
（2）利用完全平方公式化简（a-$\frac{1}{a}$）2，把（1）的结果代入计算即可求出值．
解答 解：（1）把a+$\frac{1}{a}$=$\sqrt{10}$，两边平方得：（a+$\frac{1}{a}$）2=a2+$\frac{1}{{a}^{2}}$+2=10，
则a2+$\frac{1}{{a}^{2}}$=8；
（2）（a-$\frac{1}{a}$）2=a2+$\frac{1}{{a}^{2}}$-2=8-2=6，
则a-$\frac{1}{a}$=±$\sqrt{6}$．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
8．某种出租车的收费标准是：起步价7元（即行驶距离不超过3km都需付7元车费），超过3km以后，每增加，加收2.4元（不足1km按1km计），某人乘这种车从甲地到乙地共支付车费19元，那么，他行程的最大值是（ ）
| A． | 11km | B． | 8km | C． | 7km | D． | 5km |
9．
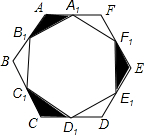如图，已知边长为2cm的正六边形ABCDEF，点A1，B1，C1，D1，E1，F1分别为所在各边的中点，则图中阴影部分的总面积是（ ）
如图，已知边长为2cm的正六边形ABCDEF，点A1，B1，C1，D1，E1，F1分别为所在各边的中点，则图中阴影部分的总面积是（ ）| A． | $\frac{3\sqrt{3}}{4}$ | B． | $\frac{2\sqrt{3}}{4}$ | C． | $\frac{\sqrt{3}}{4}$ | D． | $\frac{\sqrt{3}}{8}$ |