题目内容
13. 如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )
如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
分析 根据勾股定理,可得AC的长,根据余弦函数等邻边比斜边,可得答案.
解答 解:由勾股定理,得
AC=$\sqrt{A{D}^{2}+C{D}^{2}}$$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
cosC=$\frac{CD}{AC}$=$\frac{4}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
故选:D.
点评 本题考查了锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
1. 一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是( )
一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是( )
 一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是( )
一次函数y=kx+b的图象如图所示,不等式kx+b>0的解集是( )| A. | x>2 | B. | x>4 | C. | x<2 | D. | x<4 |
8.某种出租车的收费标准是:起步价7元(即行驶距离不超过3km都需付7元车费),超过3km以后,每增加,加收2.4元(不足1km按1km计),某人乘这种车从甲地到乙地共支付车费19元,那么,他行程的最大值是( )
| A. | 11km | B. | 8km | C. | 7km | D. | 5km |
18. 某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
频数分布表
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.
 某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:
某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表:频数分布表
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 4 |
| 第2组 | 30≤x<35 | 8 |
| 第3组 | 35≤x<40 | 16 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 10 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.
2.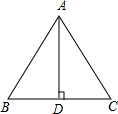 如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
 如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
如图,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )| A. | ∠B=45° | B. | ∠BAC=90° | C. | BD=AC | D. | AB=AC |
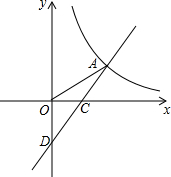 如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象在第一象限内相交于点A(m,2),交x轴、y轴分别于点C、D,且C是AD的中点,S△ODA=4.
如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象在第一象限内相交于点A(m,2),交x轴、y轴分别于点C、D,且C是AD的中点,S△ODA=4. 小明“六一”去公园玩投掷飞镖的游戏,投中图中阴影部分有奖品(飞镖被平均分成8分).小明能获得奖品的概率是$\frac{5}{8}$.
小明“六一”去公园玩投掷飞镖的游戏,投中图中阴影部分有奖品(飞镖被平均分成8分).小明能获得奖品的概率是$\frac{5}{8}$.