题目内容
11.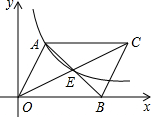 如图,?AOBC中,对角线交于点E,双曲线经过A、E两点,若?AOBC的面积为12,则k=4.
如图,?AOBC中,对角线交于点E,双曲线经过A、E两点,若?AOBC的面积为12,则k=4.
分析 过A作AD⊥OB于D,过E作EF⊥OB于F,如图,设A(x,$\frac{k}{x}$),B(a,0),根据平行四边形的性质得AE=BE,则可判断EF为△BAD的中位线,于是得到EF=$\frac{1}{2}$AD=$\frac{k}{2x}$,DF=$\frac{1}{2}$(a-x),OF=OD+DF=$\frac{a+x}{2}$,则可表示出E($\frac{a+x}{2}$,$\frac{k}{2x}$),然后根据反比例函数图象上点的坐标特征得到$\frac{a+x}{2}$,解得a=3x,然后利用平行四边形的面积公式得到关于k的方程,再解方程即可.
解答 解: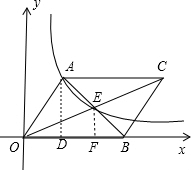 过A作AD⊥OB于D,过E作EF⊥OB于F,如图,
过A作AD⊥OB于D,过E作EF⊥OB于F,如图,
设A(x,$\frac{k}{x}$),B(a,0),
∵四边形AOBC为平行四边形,
∴AE=BE,
∴EF为△BAD的中位线,
∴EF=$\frac{1}{2}$AD=$\frac{k}{2x}$,
∴DF=$\frac{1}{2}$(a-x),
OF=OD+DF=$\frac{a+x}{2}$,
∴E($\frac{a+x}{2}$,$\frac{k}{2x}$),
∵E点在双曲线上,
∴$\frac{a+x}{2}$•$\frac{k}{2x}$=k,
∴a=3x,
∵平行四边形的面积是12,
∴AD•OB=12,
即$\frac{k}{x}$•a=12,
∴$\frac{k}{x}$•3x=12,
∴k=4.
故答案为4.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了平行四边形的性质.

练习册系列答案
相关题目
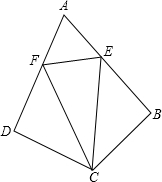 如图,在四边形ABCD中,∠ADC=∠ABC=90°,CB=CD,点E、F分别在AB、AD上,AE=AF,联结CE,CF.
如图,在四边形ABCD中,∠ADC=∠ABC=90°,CB=CD,点E、F分别在AB、AD上,AE=AF,联结CE,CF.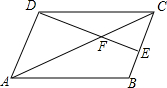 如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则四边形ABEF的面积为30.
如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则四边形ABEF的面积为30. 已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=8cm.求:
已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=8cm.求: 已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$.
已知:如图,$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$. 如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为7.
如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为7.