Question

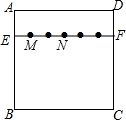
13．如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$的值等于$\frac{8}{9}$．

Answer 1

分析 根据辅助线的性质得到∠ABD=∠CBD=45°，四边形MNPQ和AEFG均为正方形，推出△BEF与△BMN是等腰直角三角形，于是得到FE=BE=AE=$\frac{1}{2}$AB，BM=MN=QM，同理DQ=MQ，即可得到结论．

解答 解：在正方形ABCD中，
∵∠ABD=∠CBD=45°，
∵四边形MNPQ和AEFG均为正方形，
∴∠BEF=∠AEF=90°，∠BMN=∠QMN=90°，
∴△BEF与△BMN是等腰直角三角形，
∴FE=BE=AE=$\frac{1}{2}$AB，BM=MN=QM，
同理DQ=MQ，
∴MN=$\frac{1}{3}$BD=$\frac{\sqrt{2}}{3}$AB，
∴$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$=$\frac{（\frac{\sqrt{2}}{3}AB）^{2}}{（\frac{1}{2}AB）^{2}}$=$\frac{8}{9}$，
故答案为：$\frac{8}{9}$．

点评 本题考查了正方形的性质，等腰直角三角形的性质，正方形的面积的计算，熟练掌握等腰直角三角形的性质是解题的关键．