题目内容
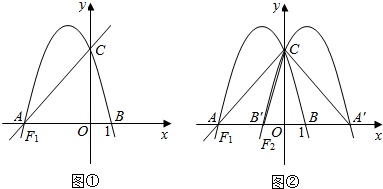
12. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{3}$ |
分析 首先证明△ACA1,△BCB1是等边三角形,推出△A1BD是直角三角形即可解决问题.
解答  解:∵∠ACB=90°,∠ABC=30°,AC=2,
解:∵∠ACB=90°,∠ABC=30°,AC=2,
∴∠A=90°-∠ABC=60°,AB=4,BC=2$\sqrt{3}$,
∵CA=CA1,
∴△ACA1是等边三角形,AA1=AC=BA1=2,
∴∠BCB1=∠ACA1=60°,
∵CB=CB1,
∴△BCB1是等边三角形,
∴BB1=2$\sqrt{3}$,BA1=2,∠A1BB1=90°,
∴BD=DB1=$\sqrt{3}$,
∴A1D=$\sqrt{{A}_{1}{B}^{2}+B{D}^{2}}$=$\sqrt{7}$.
故选A.
点评 本题考查旋转的性质、30度角的直角三角形性质、等边三角形的判定和性质、勾股定理等知识,解题的关键是证明△ACA1,△BCB1是等边三角形,属于中考常考题型.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
2.2016年3月2日--16日我国召开两会,两会参会代表实有代表2943人,2943人用科学记数法表示为( )
| A. | 2.943×102人 | B. | 29.43×102人 | C. | 2.943×103人 | D. | 2.943×104人 |
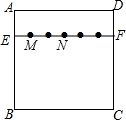 如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是5$\sqrt{3}$cm.
如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是5$\sqrt{3}$cm.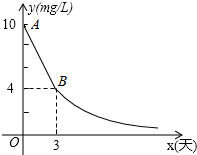 环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论: