题目内容
7. 如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是4$\sqrt{2}$.
如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是4$\sqrt{2}$.
分析 由边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,利用勾股定理的知识求出B′C的长,再根据等腰直角三角形的性质,勾股定理可求B′O,OD,从而可求四边形AB′OD的周长.
解答  解:连接B′C,
解:连接B′C,
∵旋转角∠BAB′=45°,∠BAC=45°,
∴B′在对角线AC上,
∵AB=AB′=2,
在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{2}$,
∴B′C=2$\sqrt{2}$-2,
在等腰Rt△OB′C中,OB′=B′C=2$\sqrt{2}$-2,
在直角三角形OB′C中,OC=$\sqrt{2}$(2$\sqrt{2}$-2)=4-2$\sqrt{2}$,
∴OD=2-OC=2$\sqrt{2}$-2,
∴四边形AB′OD的周长是:2AD+OB′+OD=4+2$\sqrt{2}$-2+2$\sqrt{2}$-2=4$\sqrt{2}$,
故答案为4$\sqrt{2}$.
点评 本题考查了旋转的性质、正方形的性质以及等腰直角三角形的性质.此题难度适中,注意连接B′C构造等腰Rt△OB′C是解题的关键,注意旋转中的对应关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若关于x的方程$\frac{2}{x-2}$+$\frac{x+m}{2-x}$=2的解为正数,则m的取值范围是( )
| A. | m<6 | B. | m>6 | C. | m<6且m≠0 | D. | m>6且m≠8 |
19.若两个相似三角形的面积之比为1:4,则它们的最大边的比是( )
| A. | 1:2 | B. | 1:4 | C. | 1:5 | D. | 1:16 |
 小明家、公交车站、学校在一条笔直的公路旁(小明家、学校到这条公路的距离忽略不计),一天,小明从家出发去上学,沿这条公路步行到公交车站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小明下车时发现还有4分钟上课,于是他沿这条公路跑步赶到学校(上、下车时间忽略不计),小明与家的距离s(单位:米)与他所用时间t(单位:分钟)之间的函数关系如图所示,已知小明从家出发7分钟时与家的距离为1200米,从上公交车到他到达学校共用10分钟,下列说法:
小明家、公交车站、学校在一条笔直的公路旁(小明家、学校到这条公路的距离忽略不计),一天,小明从家出发去上学,沿这条公路步行到公交车站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小明下车时发现还有4分钟上课,于是他沿这条公路跑步赶到学校(上、下车时间忽略不计),小明与家的距离s(单位:米)与他所用时间t(单位:分钟)之间的函数关系如图所示,已知小明从家出发7分钟时与家的距离为1200米,从上公交车到他到达学校共用10分钟,下列说法: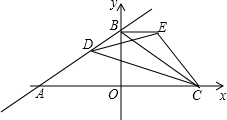 如图,直线y=$\frac{1}{2}$x+2交x轴、y轴于A、B两点,点C与点A关于y轴对称,点D是线段AB上一个动点,ED=EC,且sin∠EDC=$\frac{\sqrt{5}}{5}$.
如图,直线y=$\frac{1}{2}$x+2交x轴、y轴于A、B两点,点C与点A关于y轴对称,点D是线段AB上一个动点,ED=EC,且sin∠EDC=$\frac{\sqrt{5}}{5}$. 如图,点P是正方形ABCD内一点,连接AP、BP、CP,若BP=$\sqrt{3}$,CP=$\sqrt{30}$,∠BPA=135°,则正方形ABCD的边长为$\sqrt{39}$.
如图,点P是正方形ABCD内一点,连接AP、BP、CP,若BP=$\sqrt{3}$,CP=$\sqrt{30}$,∠BPA=135°,则正方形ABCD的边长为$\sqrt{39}$. 如图,A(x,0)、B(0,y),若|x+2y-6|+|2x+y|=0,试分别求出A、B两点的坐标.
如图,A(x,0)、B(0,y),若|x+2y-6|+|2x+y|=0,试分别求出A、B两点的坐标.