题目内容
13.若关于x的方程$\frac{2}{x-2}$+$\frac{x+m}{2-x}$=2的解为正数,则m的取值范围是( )| A. | m<6 | B. | m>6 | C. | m<6且m≠0 | D. | m>6且m≠8 |
分析 先得出分式方程的解,再得出关于m的不等式,解答即可.
解答 解:原方程化为整式方程得:2-x-m=2(x-2),
解得:x=2-$\frac{m}{3}$,
因为关于x的方程$\frac{2}{x-2}$+$\frac{x+m}{2-x}$=2的解为正数,
可得:$2-\frac{m}{3}>0$,
解得:m<6,
因为x=2时原方程无解,
所以可得$2-\frac{m}{3}≠2$,
解得:m≠0.
故选C.
点评 此题考查分式方程,关键是根据分式方程的解法进行分析.

练习册系列答案
相关题目
3.某种蔬菜按品质分成三个等级销售,销售情况如表:
则售出蔬菜的平均单价为4.4元/千克.
| 等级 | 单价(元/千克) | 销售量(千克) |
| 一等 | 5.0 | 20 |
| 二等 | 4.5 | 40 |
| 三等 | 4.0 | 40 |
18.南宁快速公交(简称:BRT)将在今年底开始动工,预计2016年下半年建成并投入试运营,首条BRT西起南宁火车站,东至南宁东站,全长约为11300米,其中数据11300用科学记数法表示为( )
| A. | 0.113×105 | B. | 1.13×104 | C. | 11.3×103 | D. | 113×102 |
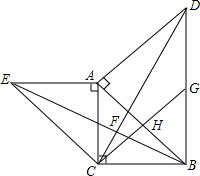 如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F. 如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:?
如图,已知经过原点的抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:? 如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是4$\sqrt{2}$.
如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是4$\sqrt{2}$.