题目内容
11.如图①,是两个全等的直角三角形硬纸板(直角边分别为a,b,斜边为c).(1)用这样的两个三角形构造成如图②的图形,请利用这个图形验证勾股定理.
(2)假设图①中的直角三角形有若干个,请运用图①中所给的直角三角形拼出另一种能验证勾股定理的图形,画出拼后的图形并利用这个图形验证勾股定理.
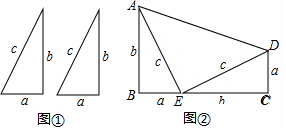
分析 (1)根据图形可知四边形ABCD是梯形,再根据梯形的面积等于三个直角三角形的面积的和,列式整理即可证明;
(2)取四个直角三角形,以斜边c为边长组成正方形,中间空出的是一个小正方形,然后利用大正方形的面积等于四个直角三角形的面积加上中间小正方形的面积,列式整理即可得证.
解答 解:(1)∵四边形ABCD是梯形,
∴梯形的面积=$\frac{1}{2}$(a+b)(a+b)=2×$\frac{1}{2}$×ab+$\frac{1}{2}$c2,
即$\frac{1}{2}$(a2+2ab+b2)=ab+$\frac{1}{2}$c2,
∴a2+b2=c2;
(2)如图所示,可以证明a2+b2=c2.
验证:大正方形的面积=4×$\frac{1}{2}$ab+(b-a)2
大正方形的面积=c2,
∴4×$\frac{1}{2}$ab+(b-a)2=c2,
整理得:a2+b2=c2.
点评 本题考查了勾股定理的证明、正方形的性质、直角三角形面积的计算;熟练掌握正方形的性质,运用面积法得出等式是解决问题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
15.下列各组数中,互为相反数的一组是( )
| A. | -|-2|与$\root{3}{-8}$ | B. | -4与-$\sqrt{(-4)^{2}}$ | C. | -$\root{3}{2}$与$\root{3}{2}$ | D. | -$\sqrt{2}$与-$\sqrt{(-2)^{2}}$ |
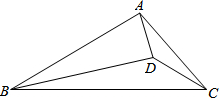 在△ABC中,AC=5$\sqrt{3}$,点D在三角形内部,连接AD、BD、CD,sin∠DCB=$\frac{1}{2}$,cos∠ABC=$\frac{\sqrt{3}}{2}$,BD=7$\sqrt{3}$,∠ABD=∠ACD,则线段AD的长度为2$\sqrt{3}$.
在△ABC中,AC=5$\sqrt{3}$,点D在三角形内部,连接AD、BD、CD,sin∠DCB=$\frac{1}{2}$,cos∠ABC=$\frac{\sqrt{3}}{2}$,BD=7$\sqrt{3}$,∠ABD=∠ACD,则线段AD的长度为2$\sqrt{3}$.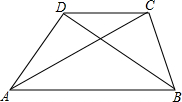 如图,已知梯形ABCD中,AB∥CD,AD>BC.求证:AC>BD.
如图,已知梯形ABCD中,AB∥CD,AD>BC.求证:AC>BD.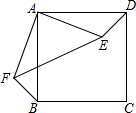 如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$.
如图,将正方形ABCD中的△ADE绕着点A顺时针旋转与△ABF重合,若AE=4,则EF的长为4$\sqrt{2}$. 如图,一位牧童每天都要从A地出发赶着牛到河边饮水,然后再到B地放牧,应该怎样选择饮水的地点,才能使牛所走的路线最短?
如图,一位牧童每天都要从A地出发赶着牛到河边饮水,然后再到B地放牧,应该怎样选择饮水的地点,才能使牛所走的路线最短?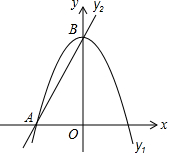 如图,已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点
如图,已知抛物线y1=-2x2+2与直线y2=2x+2交于A、B两点