题目内容
2.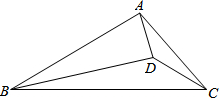 在△ABC中,AC=5$\sqrt{3}$,点D在三角形内部,连接AD、BD、CD,sin∠DCB=$\frac{1}{2}$,cos∠ABC=$\frac{\sqrt{3}}{2}$,BD=7$\sqrt{3}$,∠ABD=∠ACD,则线段AD的长度为2$\sqrt{3}$.
在△ABC中,AC=5$\sqrt{3}$,点D在三角形内部,连接AD、BD、CD,sin∠DCB=$\frac{1}{2}$,cos∠ABC=$\frac{\sqrt{3}}{2}$,BD=7$\sqrt{3}$,∠ABD=∠ACD,则线段AD的长度为2$\sqrt{3}$.
分析 延长CD交AB于E,在BD上截取BF=CA=5$\sqrt{3}$,连接AF,交DE于O,由sin∠DCB=$\frac{1}{2}$、cos∠ABC=$\frac{\sqrt{3}}{2}$知∠DCB=∠ABC=30°,继而可得BE=CE、∠BEC=120°、∠AEC=60°,再证△BEF≌△CEA得EF=EA,结合∠FEC=∠AEC=60°知EO垂直且平分AF,从而得出AD=FD=BD-BF.
解答 解:如图,延长CD交AB于E,在BD上截取BF=CA=5$\sqrt{3}$,连接AF,交DE于O,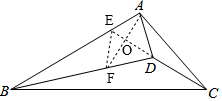
∵sin∠DCB=$\frac{1}{2}$,cos∠ABC=$\frac{\sqrt{3}}{2}$,
∴∠DCB=∠ABC=30°,
∴BE=CE,∠BEC=120°,∠AEC=60°,
在△BEF和△CEA中,
∵$\left\{\begin{array}{l}{BE=CE}\\{∠EBF=∠ECA}\\{BF=CA}\end{array}\right.$,
∴△BEF≌△CEA,
∴∠BEF=∠CEA=$\frac{1}{2}$∠BEC=60°,EF=EA,
∴∠FEC=∠BEC-∠BEF=60°,
在等腰△AEF中,∵∠FEC=∠AEC=60°,
∴EO垂直且平分AF,
∴AD=FD=BD-BF=7$\sqrt{3}$-5$\sqrt{3}$=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题主要考查全等三角形的判定与性质、等腰三角形的判定与性质、中垂线的性质等知识点,构建全等三角形是解题的关键.

练习册系列答案
相关题目
11.在0,-3,-1,5这四个数中,正数是( )
| A. | 0 | B. | -3 | C. | -1 | D. | 5 |
7.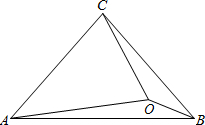 △ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )
△ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )
 △ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )
△ABC中,∠CAB=∠CBA=50°,O为△ABC内一点,∠OAB=10°,∠OBC=20°,则∠OCA的度数为( )| A. | 55° | B. | 60° | C. | 70° | D. | 80° |
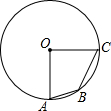 如图,已知A,B,C均在圆O上,且OA⊥OC,AB=1,BC=$\sqrt{2}$,则OABC的面积为$\frac{7}{4}$.
如图,已知A,B,C均在圆O上,且OA⊥OC,AB=1,BC=$\sqrt{2}$,则OABC的面积为$\frac{7}{4}$.